题目内容
10.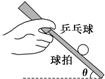 有一种游戏,游戏者手持乒乓球拍托球移动,距离大者获胜.若某人在游戏中沿水平面做匀加速直线运动,球拍与球保持相对静止且球拍平面和水平面之间的夹角为θ,如图所示.设球拍和球质量分别为M、m,不计球拍和球之间的摩擦,不计空气阻力,则( )
有一种游戏,游戏者手持乒乓球拍托球移动,距离大者获胜.若某人在游戏中沿水平面做匀加速直线运动,球拍与球保持相对静止且球拍平面和水平面之间的夹角为θ,如图所示.设球拍和球质量分别为M、m,不计球拍和球之间的摩擦,不计空气阻力,则( )| A. | 运动员的加速度大小为gtan θ | |
| B. | 球拍对球的作用力大小为mg | |
| C. | 球拍对球的作用力大小为mgcos θ | |
| D. | 运动员对球拍的作用力大小为$\frac{(M+m)g}{cosθ}$ |
分析 球、球拍和人具有相同的加速度,对球分析,根据牛顿第二定律求出加速度的大小,结合平行四边形定则求出球拍对球的作用力的大小.对整体分析,根据合力的方向确定地面对运动员的作用力方向.
解答 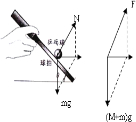 解:A、球和运动员具有相同的加速度,对小球分析如图所示,则小球所受的合力为mgtanθ,根据牛顿第二定律得:a=$\frac{mgtanθ}{m}$=gtnnθ,故A正确.
解:A、球和运动员具有相同的加速度,对小球分析如图所示,则小球所受的合力为mgtanθ,根据牛顿第二定律得:a=$\frac{mgtanθ}{m}$=gtnnθ,故A正确.
B、根据平行四边形定则知,球拍对球的作用力N=$\frac{mg}{cosθ}$,故BC错误.
D、对球拍和球整体分析,整体的合力为(M+m)a,根据平行四边形定则知,运动员对球拍的作用力为:F=$\frac{(M+m)g}{cosθ}$,故D正确.
故选:AD.
点评 解决本题的关键知道球、球拍和人具有相同的加速度,结合牛顿第二定律进行求解,掌握整体法、隔离法的运用.

练习册系列答案
相关题目
19.甲、乙两车在平直公路上沿同一方向行驶,其v-t图象如图所示,在 t=0时刻,乙车在甲车前方x0处,在t=t1时间内甲车的位移为x.下列判断正确的是( )
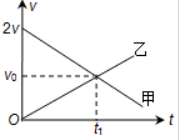

| A. | 若甲、乙在t1时刻相遇,则x0=$\frac{2}{3}$x | |
| B. | 若甲、乙在$\frac{{t}_{1}}{2}$时刻相遇,则下次相遇时刻为$\frac{3}{2}$t1 | |
| C. | 若x0=$\frac{3}{4}$x,则甲、乙一定相遇两次 | |
| D. | 若x0=$\frac{1}{2}$x,则甲、乙一定不能相遇 |
5.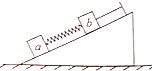 如图所示,斜面置于粗糙的水平面上,将两个相同的光滑木块a、b放在斜面上,a、b用一轻质弹簧连接,b的右端用细绳与固定在斜面上的挡板相连.达到稳定状态时a、b、斜面均静止,在细绳剪断瞬间,斜面仍保持静止,则在细绳剪断瞬间,相连说法正确的是( )
如图所示,斜面置于粗糙的水平面上,将两个相同的光滑木块a、b放在斜面上,a、b用一轻质弹簧连接,b的右端用细绳与固定在斜面上的挡板相连.达到稳定状态时a、b、斜面均静止,在细绳剪断瞬间,斜面仍保持静止,则在细绳剪断瞬间,相连说法正确的是( )
 如图所示,斜面置于粗糙的水平面上,将两个相同的光滑木块a、b放在斜面上,a、b用一轻质弹簧连接,b的右端用细绳与固定在斜面上的挡板相连.达到稳定状态时a、b、斜面均静止,在细绳剪断瞬间,斜面仍保持静止,则在细绳剪断瞬间,相连说法正确的是( )
如图所示,斜面置于粗糙的水平面上,将两个相同的光滑木块a、b放在斜面上,a、b用一轻质弹簧连接,b的右端用细绳与固定在斜面上的挡板相连.达到稳定状态时a、b、斜面均静止,在细绳剪断瞬间,斜面仍保持静止,则在细绳剪断瞬间,相连说法正确的是( )| A. | a所受的合外力一定不为零 | |
| B. | 斜面所受地面的摩擦力一定为零 | |
| C. | b所受的合外力一定不为零 | |
| D. | 斜面所受地面的支持力小于a、b和斜面的总重力 |
20.一个电荷量为1.0×10-7C的负电荷从电场中A点移动到B点时电场力做功2.0×10-7J,从C点移动到D点时克服电场力做功7.0×10-7J.若已知B点比C点的电势高3V,则下列关于各点间的电势差关系正确的是( )
| A. | UAB=2V | B. | UCD=-7V | C. | UBD=-3V | D. | UAC=1V |
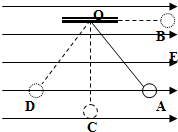 如图,质量为m的带电小球用长L为的绝缘细绳系在O点,绳的形变可以不计,空间存在水平向右的匀强电场,电场强度为E,静止时位于A点,此时绳与竖直方向夹30°的角.现将小球从绳拉直且水平的B点释放,求
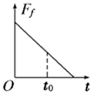
如图,质量为m的带电小球用长L为的绝缘细绳系在O点,绳的形变可以不计,空间存在水平向右的匀强电场,电场强度为E,静止时位于A点,此时绳与竖直方向夹30°的角.现将小球从绳拉直且水平的B点释放,求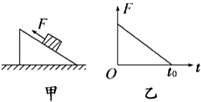 如图甲所示,一物块放在粗糙斜面上,在平行斜面向上的外力F作用下斜面和物块始终处于静止状态,当F按图乙所示规律变化时,物块与斜面间的摩擦力大小变化规律可能是如图答案中的( )
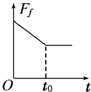
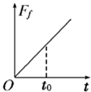
如图甲所示,一物块放在粗糙斜面上,在平行斜面向上的外力F作用下斜面和物块始终处于静止状态,当F按图乙所示规律变化时,物块与斜面间的摩擦力大小变化规律可能是如图答案中的( )
 如图所示,物体A重40N,物体B重20N,A与B、A与水平地面间的动摩擦因数为0.4,物体B用细绳系住,细绳另一端固定在竖直墙上且细绳始终保持水平.在A上施加水平拉力F,求F为多大时,才能将物体A匀速拉出?
如图所示,物体A重40N,物体B重20N,A与B、A与水平地面间的动摩擦因数为0.4,物体B用细绳系住,细绳另一端固定在竖直墙上且细绳始终保持水平.在A上施加水平拉力F,求F为多大时,才能将物体A匀速拉出?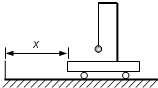 如图所示,小车上有一个固定支架,支架上用长为L的绝缘细线悬挂质量为m、电量为+q的小球,处于水平方向的匀强电场中(图中未画出),小车在竖直固定挡板右侧某处,向着挡板从静止开始做加速度a=g的匀加速直线运动,此过程细线刚好保持竖直,当小车碰到挡板就立即停止运动,且此时电场方向为竖直向下,电场强度大小保持不变.求小车停止后.
如图所示,小车上有一个固定支架,支架上用长为L的绝缘细线悬挂质量为m、电量为+q的小球,处于水平方向的匀强电场中(图中未画出),小车在竖直固定挡板右侧某处,向着挡板从静止开始做加速度a=g的匀加速直线运动,此过程细线刚好保持竖直,当小车碰到挡板就立即停止运动,且此时电场方向为竖直向下,电场强度大小保持不变.求小车停止后.