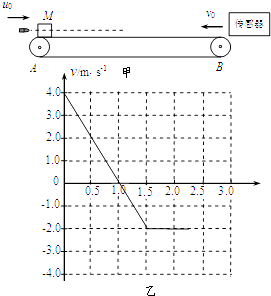
��Ŀ����
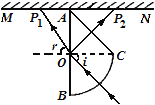
����Ŀ��ͼʾΪij�������ʵĽ���ͼ����AOCΪ����ֱ����������BCΪ�뾶R��10cm���ķ�֮һԲ����AB��ˮƽ��ĻMN��ֱ���Ӵ���A�㡣�ɺ����Ϲ����ֵ�ɫ����ɵ�ϸ����ɫ������Բ��O����AB�ֽ����ϵ������i=45�㣬�����ˮƽ��ĻMN�ϳ����������ߣ����������ֱ�ΪP1��P2������ý��ʶԺ����Ϲ�������ʷֱ�Ϊn1 = ![]() ��n2 =
��n2 =![]() ��
��

��1���ж�P1��P2�����������ߵ���ɫ��
��2������������ľ���P1P2��
���𰸡���1������P1Ϊ��ɫ������P2Ϊ��ɫ����ɫ�Ļ��ɫ��2��P1P2 = (5![]() + 10)cm
+ 10)cm
��������
�����������1����ý��ʶԺ����Ϲ���ٽ�Ƿֱ�ΪC1��C2����
sinC1=![]() =
= ![]() ��1�֣�
��1�֣�
��C1��60�� ��1�֣�
ͬ��C2��45�� ��1�֣�
i = 45�� = C2��i = 45��< C1
�����Ϲ���AB�淢��ȫ���䣬�������AB��һ�������䣬һ���ַ��䣬���ɼ��ι�ϵ��֪�����������AC��ֱ����������P1Ϊ��ɫ�� ��1�֣�
����P2Ϊ��ɫ����ɫ�Ļ��ɫ�� ��1�֣�
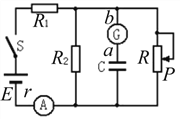
��2��������ͼ��·ͼ���������Ϊr���������䶨����
n1 = ![]() ��1�֣�
��1�֣�
��sinr = ![]() ��1�֣�
��1�֣�
�ɼ���֪ʶ�ɵ�tanr = ![]() ��1�֣�
��1�֣�
���AP1 = 5![]() cm ��1�֣�
cm ��1�֣�
�ɼ���֪ʶ�ɵ���AOP2Ϊ����ֱ��������
��� AP2=10cm
����P1P2 = (5![]() + 10)cm ��1�֣�
+ 10)cm ��1�֣�

 ��У����ϵ�д�
��У����ϵ�д�