��Ŀ����
����Ŀ����ͼ����ʾ��ˮƽ����A��B���ּ�ľ���L=3.0m������M=1.0kg����飨����Ϊ�ʵ㣩�洫�ʹ�һ���Ժ㶨������v0���������˶���������˶��������ʱ������m=0.020kg���ӵ���u0=400m/s��ˮƽ�ٶ�����������鲢�������ڴ��ʹ����Ҷ���һ�������������鱻��������ٶ���ʱ��ı仯��ϵ��ͼ����ʾ��ͼ��ȡ�����˶��ķ���Ϊ�������ӵ��������˲��Ϊt=0ʱ�̣������ӵ���������ʱ��ɺ��Բ��ƣ����ӵ�������д�����������Σ�գ��������������ӵ������������ı䣮���ƿ���������A��B�ֵĴ�С��ȡ�������ٶ�g=10m/s2 �� 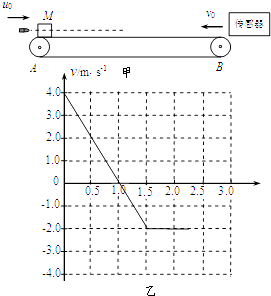
��1��������봫�ʹ���Ķ�Ħ�������̣�
��2�����ӵ��������Ĺ����в���������Q1��
��3������ӵ�һ���ӵ�������鿪ʼ��ÿ����t=1.5s����һ����ͬ���ӵ���ͬ�����ٶȻ�����飬ֱ����������뿪���ʹ����������ӵ�������������������ͬ������������������봫����֮����Ħ������������Q2 ��
���𰸡�
��1����:�����ٶ�ͼ���֪������ڻ���Ħ���������������ȱ����˶�����0��1s�������ٶ���4m/s��Ϊ0��
�˹������ļ��ٶȴ�С ![]() =4.0 m/s2
=4.0 m/s2
��ţ�ٵڶ������� f=��mg=ma ��� ![]() =0.40
=0.40
������봫�ʹ���Ķ�Ħ��������Ϊ0.4
��2����:��鱻����ǰ���ٶȴ�СΪv0=2.0m/s�����ٶ�ͼ���֪��鱻������˲�������ٶȴ�Сv=4.0m/s���������ң�
���ӵ�����������ٶ�Ϊu��������Ϊ������
���ݶ����غ㶨���� mu0��Mv0=mu+Mv
��� u= ![]() =100 m/s
=100 m/s
���������غ��� Q1= ![]() =1.49��103 J
=1.49��103 J
�����ӵ��������Ĺ����в���������Q1Ϊ1.49��103 J
��3����:��1���ӵ�����������������˶���ʱ��Ϊt1=1.0 s���������˶���������Ϊx1����x1= ![]() t1=2.0 m��
t1=2.0 m��
1.0sʱ����Ϊ�����˶����˶�ʱ��Ϊt2=0.50s��λ�ƴ�СΪx2= ![]() t2=0.50m
t2=0.50m
�����ڡ�t=1.5sʱ���ڣ���������˶��ľ���Ϊl=x1��x2=1.5m
�ڡ�t=1.5sʱ���ڣ������Դ��ʹ���λ��Ϊ��x1=l+x3=4.5m
��t=1.5sʱ�����ٶ��봫�ʹ��ٶ���ͬ�����Եڶ����ӵ�����������˶�������һ���ӵ����������˶������ͬ�������˶��Ŀ��ܴﵽ��������Ϊ2.0m��
����ʱ����봫�ʹ��Ҷ˾���Ϊl=1.5m��������еڶ����ӵ��������ʹ���
����鱻�ڶ����ӵ����������ڴ��ʹ��ϻ��е�ʱ��Ϊt3
�����˶�ѧ��ʽ����l=vt3 ![]() at32
at32
��ã�t3=0.50s
���ڶ��α���������Դ��ʹ���λ�ơ�x2=��l+v0t3=2.5m
����Q2=��mg����x1+��x2��=28J
������ӵ�һ���ӵ�������鿪ʼ��ÿ����t=1.5s����һ����ͬ���ӵ���ͬ�����ٶȻ�����飬ֱ����������뿪���ʹ����������ӵ�������������������ͬ����������������봫����֮����Ħ������������Q2Ϊ28J
���������ӵ�����ľ���˲�䶯���غ㣬�ö����غ㶯�����ľ�����ҵij��ٶȣ�ľ���ڴ��ʹ������ȼ���ֱ���˶������ٶ�ʱ���ϵʽ���1s����ٶȣ������봫�ʹ����ٶȱȽϣ��ж�ľ���Ƿ��Ѿ��ﵽ���٣������Խ���˹�����ľ�������˶��������룻��һ���������ö����غ㶨�����һ���̱Ƚϣ�ľ��ʹ��ʹ�����Ħ���������������ڻ���Ħ��������ľ���봫�ʹ�֮������λ�ƣ�