��Ŀ����
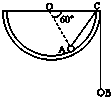 ��2009?բ������ģ����ͼ��ʾ��һ���뾶ΪR�İ����ε���̶��������ϣ����ˮƽ��O��Ϊ�����ģ�����ڱ��漰����ǹ⻬�ģ�һ������ϸ�߿�������ϣ��ߵ����˷ֱ�ϵ��С��A��B�������Ǵ���ƽ��״̬ʱ��С��A��O���������ˮƽ�ߵļн�Ϊ60�㣮
��2009?բ������ģ����ͼ��ʾ��һ���뾶ΪR�İ����ε���̶��������ϣ����ˮƽ��O��Ϊ�����ģ�����ڱ��漰����ǹ⻬�ģ�һ������ϸ�߿�������ϣ��ߵ����˷ֱ�ϵ��С��A��B�������Ǵ���ƽ��״̬ʱ��С��A��O���������ˮƽ�ߵļн�Ϊ60�㣮��1����С��A��С��B��������mA��mB
��2�������⣺�ֽ�A��������Ϊ2m��B��������Ϊm���ҿ�ʼʱA��λ�����C�㣬�ɾ�ֹ�����»�����A�����ʱ�������������Ϊ���
ijͬѧ�ⷨ���£���A�����ʱ��A���½��ĸ߶�ΪR��B�������ĸ߶�Ϊ
| 2 |
| 2 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
����Ϊ���������Ƿ���ȷ���������Ϊ��ȷ������ɴ��⣻�������Ϊ����ȷ����ָ������������ȷ�Ľ��
��������1���ȶ�mB������������������������������ƽ�⣬����������ٶ�mA���������������ݹ�����ƽ��������ʽ��⣮
��2��A�������ʱ��vA������vB��Ӧ��vA�����ʹ�ֱ�����ķ���ֽ⣬�����ӷ���ķ��ٶȼ�������B����ٶ�vB�Ĵ�С���ٸ��ݻ�е���غ㶨����ʽ�����
��2��A�������ʱ��vA������vB��Ӧ��vA�����ʹ�ֱ�����ķ���ֽ⣬�����ӷ���ķ��ٶȼ�������B����ٶ�vB�Ĵ�С���ٸ��ݻ�е���غ㶨����ʽ�����
����⣺��1������������ΪT�����A��ĵ���ΪN�����ݶԳ��Կɵã�N=T
��ƽ��������2Tcos30��=mAg
��B��������������ƽ��ã�T=mBg
�����ã�mA��mB=
��1
��2������ȷ��
A�������ʱ��vA������vB��Ӧ��vA�����ʹ�ֱ�����ķ���ֽ⣬�����ӷ���ķ��ٶȼ�������B����ٶ�vB�Ĵ�С��
����vB=vAsin45��=
vA
���ݻ�е���غ㶨���У�mAgR-mBg
R=
mA
+
mB
mAgR-mBg
R=
mA
+
mB(
vA)2
�ɵã�vA=
vB=
�𣺣�1��С��A��С��B��������Ϊ��mA��mB=
��1��
��2������ȷ�����������Ϊ��vA=
vB=
��
��ƽ��������2Tcos30��=mAg
��B��������������ƽ��ã�T=mBg
�����ã�mA��mB=
| 3 |
��2������ȷ��
A�������ʱ��vA������vB��Ӧ��vA�����ʹ�ֱ�����ķ���ֽ⣬�����ӷ���ķ��ٶȼ�������B����ٶ�vB�Ĵ�С��
����vB=vAsin45��=
| ||
| 2 |
���ݻ�е���غ㶨���У�mAgR-mBg
| 2 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
| 2 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| ||
| 2 |
�ɵã�vA=
|
|
�𣺣�1��С��A��С��B��������Ϊ��mA��mB=
| 3 |
��2������ȷ�����������Ϊ��vA=
|
|
�����������Ǽ����������⣬�ȷ�������������壬�ٷ��������ϸ��ӵ���һ�����壬ͬʱҪ���������ֽⷨ������Ϊ���㣮
ע��������������������ٶȴ�С��һ����ȣ�ҪӦ���ٶȵķֽ��������С������ʹ�ϵ��
ע��������������������ٶȴ�С��һ����ȣ�ҪӦ���ٶȵķֽ��������С������ʹ�ϵ��

��ϰ��ϵ�д�
�����Ŀ
 ��2009?բ������ģ����ͼ��ʾ����ƿ�ڷ��һ���������������壬��ƿ�������Ϊ800mL�������U�ι������е�ˮ������ƽ����ƿ����ˮ���¶�Ϊ27�棬����ע��������ƿ��ע��200mLˮʱ��U�ι������е�ˮ�������25cm�߶ȲȻ����ƿ�������ȣ�ʹ�����¶ȱ�Ϊ57�森����ϸ���е������������
��2009?բ������ģ����ͼ��ʾ����ƿ�ڷ��һ���������������壬��ƿ�������Ϊ800mL�������U�ι������е�ˮ������ƽ����ƿ����ˮ���¶�Ϊ27�棬����ע��������ƿ��ע��200mLˮʱ��U�ι������е�ˮ�������25cm�߶ȲȻ����ƿ�������ȣ�ʹ�����¶ȱ�Ϊ57�森����ϸ���е������������ ��2009?բ������ģ����ͼ��ʾ����ǿΪE����ǿ�糡����A��B��C���㣬�������һ���ȱ������Σ��߳�Ϊ0.1m���ױ�AC�͵糡�ߵķ���ƽ�У��ְѵ���Ϊ2��10-8C�ĸ���ɴ�A���Ƶ�B�㣬�˷��糡������4��10-5J����E�Ĵ�СΪ
��2009?բ������ģ����ͼ��ʾ����ǿΪE����ǿ�糡����A��B��C���㣬�������һ���ȱ������Σ��߳�Ϊ0.1m���ױ�AC�͵糡�ߵķ���ƽ�У��ְѵ���Ϊ2��10-8C�ĸ���ɴ�A���Ƶ�B�㣬�˷��糡������4��10-5J����E�Ĵ�СΪ