题目内容
（2009?闸北区二模）如图所示，烧瓶内封闭一定质量的理想气体，烧瓶的总体积为800mL，最初，U形管两臂中的水银面齐平，烧瓶中无水，温度为27℃，当用注射器往烧瓶中注入200mL水时，U形管两臂中的水银面出现25cm高度差，然后将烧瓶缓慢加热，使气体温度变为57℃．忽略细管中的气体体积．求：（1）大气压强P0为多少cmHg？
（2）最终U形管两臂中的水银面的高度差？
分析：①气体发生等温变化，已知气体体积，由玻意耳定律可以求出气体压强．
②根据查理定律求出气体的压强，然后由平衡条件求出水银面的高度差．
②根据查理定律求出气体的压强，然后由平衡条件求出水银面的高度差．
解答：解：（1）由题意知：P1=P0，P2=P0+h=P0+25cmHg，V1=800mL，V2=600mL，
由玻意耳定律可得：P1V1=P2V2，
即：p0×800=（p0+25）×600
代入数据，解得p0=75cmHg
（2）由题意知：P2=75cmHg+25cmHg=100cmHg，T2=27+273=300K，T3=57+273=330K，
根据查理定律可得
=
即
=
解得p3=110cmHg
所以△h=（110-75）cm=35cm．
答：（1）大气压强P0为75cmHg．
（2）最终U形管两臂中的水银面的高度差为35cm．
由玻意耳定律可得：P1V1=P2V2，
即：p0×800=（p0+25）×600
代入数据，解得p0=75cmHg
（2）由题意知：P2=75cmHg+25cmHg=100cmHg，T2=27+273=300K，T3=57+273=330K，
根据查理定律可得
| p2 |
| T2 |
| p3 |
| T3 |
即
| 100 |
| 300 |
| p3 |
| 330 |
解得p3=110cmHg
所以△h=（110-75）cm=35cm．
答：（1）大气压强P0为75cmHg．
（2）最终U形管两臂中的水银面的高度差为35cm．
点评：本题考查了求气体压强与体积问题，根据题意确定初末状态的状态参量、熟练应用玻意耳定律和查理定律即可正确解题；本题难度不大，是一道基础题．
练习册系列答案
相关题目
（2009?闸北区二模）如图所示，场强为E的匀强电场中有A、B、C三点，三点组成一个等边三角形，边长为0.1m，底边AC和电场线的方向平行．现把电量为2×10-8C的负电荷从A点移到B点，克服电场力做功4×10-5J，则E的大小为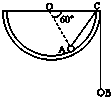
（2009?闸北区二模）如图所示，一个半径为R的半球形的碗固定在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的．一根轻质细线跨在碗口上，线的两端分别系有小球A和B，当它们处于平衡状态时，小球A与O点的连线与水平线的夹角为60°．