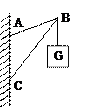题目内容
河宽d=100m,水流速度υ1=3m/s,船在静水中的速度是4m/s,求:
(1)欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移是多大?
(2)欲使船航行距离最短,船应怎样渡河?渡河时间多长?
(1)欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移是多大?
(2)欲使船航行距离最短,船应怎样渡河?渡河时间多长?
设船与岸成θ角向对岸行驶,如图所示,则当船行到对岸时,s2=
t=
=
当sinθ=1时,t最小,即船应沿垂直与河岸的方向渡河.
tmin=
=
s=25s;
船经过的位移大小:s=vct;
vc=
=5m/s;
解得:s=5×25=125m;
(2)欲使船航行距离最短,需使船的实际位移(合位移)与河岸垂直,设此时船的开行速度υ2与岸成?角,如图1-2所示.
则cos?=
=
,
υ=
=
m/s=
m/s,
t=
=
s=
s
答:(1)欲使船渡河时间最短,船应垂直河岸渡河,最短时间是25s,船经过的位移是125m;
(2)欲使船航行距离最短,船的合速度垂直河岸渡河,渡河时间
s.
| d |
| sinθ |
t=
| s2 |
| v2 |
| d |
| v2sinθ |
当sinθ=1时,t最小,即船应沿垂直与河岸的方向渡河.

tmin=
| d |
| v2 |
| 100 |
| 4 |
船经过的位移大小:s=vct;
vc=
|
解得:s=5×25=125m;
(2)欲使船航行距离最短,需使船的实际位移(合位移)与河岸垂直,设此时船的开行速度υ2与岸成?角,如图1-2所示.

则cos?=
| υ1 |
| υ2 |
| 3 |
| 4 |
υ=
| υ22-υ12 |
| 42-32 |
| 7 |
t=
| d |
| υ |
| 100 | ||
|
100
| ||
| 7 |
答:(1)欲使船渡河时间最短,船应垂直河岸渡河,最短时间是25s,船经过的位移是125m;
(2)欲使船航行距离最短,船的合速度垂直河岸渡河,渡河时间
100
| ||
| 7 |

练习册系列答案
相关题目
如图所示,已知两个共点力的合力为50N,分力F1的方向与合力F的方向成30°角,分力F2的大小为60N,则( )
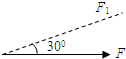
| A.F1的大小是唯一的 | B.F2的方向是唯一的 |
| C.F2有两个可能的方向 | D.F2可取任意方向 |

 ,
,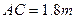 ,
, ,在B点挂一重物,
,在B点挂一重物,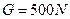 ,求AB、BC上的受力。
,求AB、BC上的受力。