题目内容
【题目】如图所示，两段光滑圆弧轨道半径分别为R1和R2，圆心分别为O1和O2，所对应的圆心角均小于5°，在最低点O平滑连接。M点和N点分别位于O点左右两侧，距离MO小于NO。现分别将位于M点和N点的两个小球A和B（均可视为质点）同时由静止释放。关于两小球第一次相遇点的位置，下列判断正确的是（）
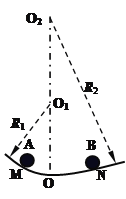
A. 一定在O点的右侧 B. 恰好在O点
C. 一定在O点的左侧 D. 条件不足，无法确定
【答案】A
【解析】据题意，两段光滑圆弧所对应的圆心角均小于5°，把两球在圆弧上的运动看做等效单摆，等效摆长等于圆弧的半径，则M、N两球的运动周期分别为
， 
两球第一次到达O点的时间分别为
， 
，由于R1＜R2，则 tM＜tN，故两小球第一次相遇点的位置一定在O点的右侧．故选A.
练习册系列答案
名校课堂系列答案
相关题目
