题目内容
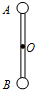如图所示，长为2L的轻杆，两端各固定一小球，A球质量为m1，B球质量为m2，过杆的中点O有一水平光滑固定轴，杆可绕轴在竖直平面内转动．当转动到竖直位置且A球在上端，B球在下端时杆的角速度为ω，此时杆对转轴的作用力为零，则A、B两小球的质量之比为（ ）分析：本题中两球均做圆周运动，其合力均充当向心力；杆对转轴的作用力为零时，杆受两球的力二力平衡，故均为拉力！
解答：解：两球均做圆周运动，合力充当向心力，设杆对球的拉力均为F；
对A球：F+m1g=m1ω2L ①；
对B球：F-m2g=m2ω2L ②；
由①②两式解得，m1：m2=（Lω2+g）：（Lω2-g）；
故选D．
对A球：F+m1g=m1ω2L ①；
对B球：F-m2g=m2ω2L ②；
由①②两式解得，m1：m2=（Lω2+g）：（Lω2-g）；
故选D．
点评：本题关键要对两球分别受力分析，找出其向心力来源，根据牛顿第二定律列式求解；由于杆受力平衡，且与转轴间无弹力，故两球对杆均为拉力，且平衡！
练习册系列答案
相关题目
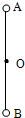如图所示，长为2L的轻杆，两端各固定一小球，A球质量为m1，B球质量为m2，且m1＞m2，过杆的中点O有一水平光滑固定轴，杆可在不同的初始条件下绕轴在竖直平面内转动．下列说法中正确的是（ ）
如图所示，长为2L的板面光滑且不导电的平板小车C放在光滑水平面上，车的右端有档板，车的质量mC=4m．今在静止的平板车的左端放一个带电量为+q．质量为m的物块A，在中间位置放一个绝缘物体B，质量为mB=2m．在整个空间加上一个水平方向的匀强电场时，金属块A由静止开始向右运动，并以速度v0与B发生碰撞，碰后A以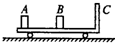
（2005?深圳一模）如图所示，长为2L的板面光滑且不导电的平板小车C放在光滑水平面上，车的右端有挡板，车的质量mC=4m．今在静止的平板车的左端放一个带电荷量为+q、质量为mA=m的金属块A，另将一绝缘小物块B放在平板车的中央，物块B的质量mB=2m．在整个空间加上一个水平方向的匀强电场时，金属块A由静止开始向右运动，A以速度v0与B发生碰撞，碰后A以v0/4的速度反弹回来，B以一定速度沿平板向右运动与C车的挡板相碰．碰后小车的速度等于碰前物块B速度的一半．物块A、B均视为质点，A、B相碰时的相互作用力远大于电场力．求：