题目内容
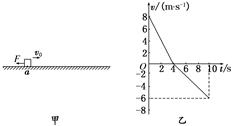
(12分)一宇宙空间探测器从某一星球表面垂直升空,假设探测器的质量恒为1500kg,发动机的推力为恒力,宇宙探测器升空到某一高度时,发动机突然关闭,如图为其速度随时间的变化规律,求:
⑴宇宙探测器在该行星表面能达到的最大高度;
⑵计算该行星表面的重力加速度;
⑶假设行星表面没有空气,试计算探测器的发动机工作时的推力大小。
⑴Hm=768m;⑵g=4m/s2;⑶F=18000N
解析试题分析:⑴在v-t图象中,图线与时间轴所围的面积表示了物体的位移,在时间轴的上方,面积为正,在时间轴的下方,面积为负,由v-t图象可知,宇宙探测器在该行星表面能达到的最大高度为:Hm=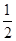 ×24×64m=768m
×24×64m=768m
⑵当关闭发动机后,探测器仅在行星对它的重力mg作用下做匀变速直线运动,在v-t图象中,图线的斜率表示了其运动的加速度,根据牛顿第二定律有:a2=-g= m/s2
m/s2
解得该行星表面的重力加速度为:g=4m/s2
⑶由图线OA段可知,发动机工作时探测器加速度为:a1= =8m/s2
=8m/s2
根据牛顿第二定律有:F-mg=ma1
解得探测器的发动机工作时的推力为:F=m(g+a1)=1500×(4+8)N=18000N
考点:本题主要考查了对v-t图象的理解及牛顿第二定律的应用问题,属于中档题。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
一个质点运动的速度一时间图象如图甲所示,在任意很短时间△t内,质点的运动可以近似视为匀速直线运动,该时间内质点的位移即为条形阴影区域的面积,经过累积,图线与横坐标轴围成的面积即为质点在相应时间内的位移。利用这种微元累积法我们可以研究许多物理问题,图乙是某物理量y随时间t变化的图象,关于此图线与横坐标轴所围成的面积,下列说法中不正确的是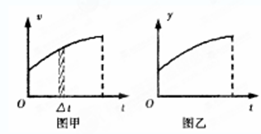
| A.如果y轴表示物体的加速度大小,则面积等于该物体在相应时间内的速度变化量 |
| B.如果y轴表示力做功的功率,则面积小于该力在相应时间内所做的功 |
| C.如果y轴表示流过用电器的电流,则面积等于在相应时间内流过该用电器的电荷量 |
| D.如果y轴表示变化的磁场在金属线圈中产生的感应电动势,则面积等于该磁场在相应时间内磁感应强度的变化量 |
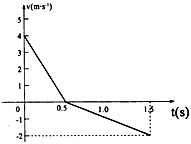
一个沿竖直方向运动的物体,其速度图象如右图所示,设向上为正方向.则可知( )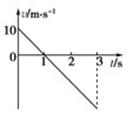
| A.这是竖直下抛运动 |
| B.这是竖直上抛又落回原地的过程 |
| C.这是从高台上竖直上抛又落回地面的过程 |
| D.抛出后3 s物体又落回抛出点 |