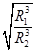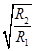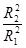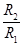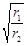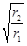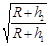题目内容
如图所示,离质量为M、半径为R、密度均匀的球体表面R远处有一质量为m的质点,此时M对m的万有引力为F1 ;当从M中挖去一半径为r=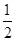 R的球体时,剩下部分对m的万有引力为F2.则F1与F2之比是多少?
R的球体时,剩下部分对m的万有引力为F2.则F1与F2之比是多少?
 R的球体时,剩下部分对m的万有引力为F2.则F1与F2之比是多少?
R的球体时,剩下部分对m的万有引力为F2.则F1与F2之比是多少?
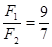
解:质点与大球球心相距2R,其万有引力为F1,则F1=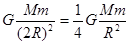 (3分
(3分
大球质量M=ρ×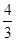 πR 3,挖去的小球质量M′=ρ×
πR 3,挖去的小球质量M′=ρ×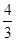 π(
π(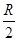 )3
)3
,即M′=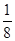 ρ×
ρ×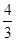 πR3=
πR3=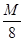
小球球心与质点间相距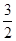 R,小球与质点间的万有引力为:
R,小球与质点间的万有引力为:
F1′=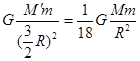 (4分)
(4分)
则剩余部分对质点m的万有引力为:
F2=F1-F1′=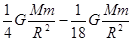 =
=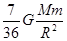 (3分)
(3分)
故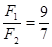 . (2分)
. (2分)
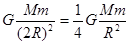 (3分
(3分大球质量M=ρ×
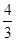 πR 3,挖去的小球质量M′=ρ×
πR 3,挖去的小球质量M′=ρ×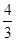 π(
π(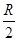 )3
)3 ,即M′=
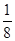 ρ×
ρ×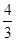 πR3=
πR3=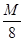
小球球心与质点间相距
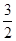 R,小球与质点间的万有引力为:
R,小球与质点间的万有引力为:F1′=
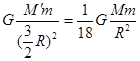 (4分)
(4分)则剩余部分对质点m的万有引力为:
F2=F1-F1′=
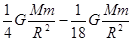 =
=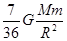 (3分)
(3分)故
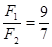 . (2分)
. (2分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
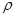 。
。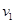 、
、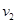 。则
。则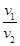 等于( )
等于( )