题目内容
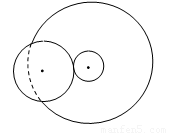
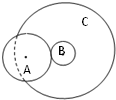
 如图,轮A和轮B之间无相对滑动,轮B和轮C共轴转动.已知轮B的半径为r,轮A半径为2r,轮C半径为4r,当轮A匀速转动时,轮A、B、C边缘上的三个点( )
如图,轮A和轮B之间无相对滑动,轮B和轮C共轴转动.已知轮B的半径为r,轮A半径为2r,轮C半径为4r,当轮A匀速转动时,轮A、B、C边缘上的三个点( )分析:同缘传动边缘点线速度相等;同轴传动角速度相等;根据公式v=rω列式求解.
解答:解:轮A与轮B同缘传动,边缘点线速度相等,故vA=vB;
轮B与轮C同轴传动,角速度相等,故ωB=ωC;
A、轮B与轮C的线速度之比为
=
=
,故vA:vB:vC=1:1:4,故A正确;
B、轮A和轮B的角速度之比为
=
=
,故ωA:ωB:ωC=1:2:2,故B错误;
C、根据a=ω2r=ωv,加速度之比为1:2:8,故C正确;
D、根据T=
,周期与角速度成反比,故周期之比为2:1:1,故D错误;
故选AC.
轮B与轮C同轴传动,角速度相等,故ωB=ωC;
A、轮B与轮C的线速度之比为
| vB |
| vC |
| rωB |
| 4r?ωC |
| 1 |
| 4 |
B、轮A和轮B的角速度之比为
| ωA |
| ωB |
| ||
|
| 1 |
| 2 |
C、根据a=ω2r=ωv,加速度之比为1:2:8,故C正确;
D、根据T=
| 2π |
| ω |
故选AC.
点评:本题关键明确两种特殊的传动(同缘传动和同轴传动)的特点,然后结合公式v=rω列式求解,基础题.

练习册系列答案
相关题目
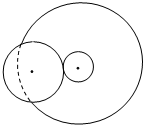
 如图,轮A和轮B之间无相对滑动,轮B和轮C共轴转动.已知轮B的半径为r,A半径为2r,轮C半径为4r,当轮A匀速转动时,轮A、B、C边缘上的三个点( )
如图,轮A和轮B之间无相对滑动,轮B和轮C共轴转动.已知轮B的半径为r,A半径为2r,轮C半径为4r,当轮A匀速转动时,轮A、B、C边缘上的三个点( )