题目内容
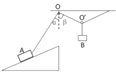
【题目】如图所示,质量为m的物块A被轻质细绳系住斜吊着放在倾角为30°的静止斜面上,物块A与斜面间的动摩擦因数为μ(μ=![]() ).细绳绕过定滑轮O,左右两边与竖直方向的夹角α=30°、β=60°,细绳右端固定在天花板上,
).细绳绕过定滑轮O,左右两边与竖直方向的夹角α=30°、β=60°,细绳右端固定在天花板上,![]() 为细绳上一光滑动滑轮,下方悬挂着重物B.整个装置处于静止状态,重力加速度为g,认为最大静摩擦力等于滑动摩擦力.
为细绳上一光滑动滑轮,下方悬挂着重物B.整个装置处于静止状态,重力加速度为g,认为最大静摩擦力等于滑动摩擦力.
(1)重物B质量为多少时,A与斜面间恰好没有摩擦力?
(2)重物B质量满足什么条件时,物块A不会滑动?
【答案】(1) ![]() (2)0≤
(2)0≤![]() ≤
≤![]() m
m
【解析】
(1)先对物体A受力分析,根据共点力平衡条件列式求解细线的拉力,再物体B和动滑轮整体分析,根据平衡条件列式求解重物B的质量。(2)A与斜面间恰好没有摩擦力作用时,先对物体A分析,根据平衡条件求解细线的拉力,再对A和斜面体整体分析,根据平衡条件求解水平地面对斜面的摩擦力。(3)考虑物体A恰好不上滑和恰好不下滑的两个临界情况,对物体A根据平衡条件求解细线的拉力,而由第一问分析知,细线的拉力等于物体B的重力。
(1)对A受力分析可知:
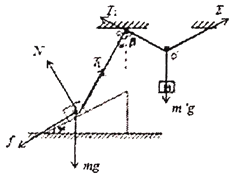
A与斜面间恰好没有摩擦力作用,即为:
![]()
根据平衡条件:
![]()
解得:
![]()
由O ′平衡,根据几何关系可知
![]()
故
![]()
(2)物体不可能下滑,物体A恰好不上滑,则对A,平行斜面方向:
![]()
垂直斜面方向:
![]()
又
![]()
解得:
![]() =
=![]() mg
mg

练习册系列答案
相关题目