题目内容
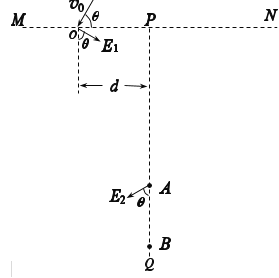
【题目】如图所示,竖直面内有水平线MN与竖直线PQ交于P点,O在水平线MN上,OP间距为d,一质量为m、电量为q的带正电粒子,从O处以大小为v0、方向与水平线夹角为θ=60的速度,进入大小为E1的匀强电场中,电场方向与竖直方向夹角为θ=60,粒子到达PQ线上的A点时,其动能为在O处时动能的4倍.当粒子到达A点时,突然将电场改为大小为E2,方向与竖直方向夹角也为θ=60的匀强电场,然后粒子能到达PQ线上的B点.电场方向均平行于MN、PQ所在竖直面,图中分别仅画出一条电场线示意其方向。已知粒子从O运动到A的时间与从A运动到B的时间相同,不计粒子重力,已知量为m、q、v0、d.求:
(1)粒子从O到A运动过程中,电场力所做功W;
(2)匀强电场的场强大小E1、E2;
(3)粒子到达B点时的动能EkB.
【答案】(1)![]() (2)E1=
(2)E1=![]() E2=
E2=![]() (3) EkB=
(3) EkB=![]()
【解析】
(1)对粒子应用动能定理可以求出电场力做的功。
(2)粒子在电场中做类平抛运动,应用类平抛运动规律可以求出电场强度大小。
(3)根据粒子运动过程,应用动能计算公式求出粒子到达B点时的动能。
(1) 由题知:粒子在O点动能为Eko=![]() 粒子在A点动能为:EkA=4Eko,粒子从O到A运动过程,由动能定理得:电场力所做功:W=EkA-Eko=
粒子在A点动能为:EkA=4Eko,粒子从O到A运动过程,由动能定理得:电场力所做功:W=EkA-Eko=![]() ;
;
(2) 以O为坐标原点,初速v0方向为x轴正向,
建立直角坐标系xOy,如图所示

设粒子从O到A运动过程,粒子加速度大小为a1,
历时t1,A点坐标为(x,y)
粒子做类平抛运动:x=v0t1,y=![]()
由题知:粒子在A点速度大小vA=2v0,vAy=![]() ,vAy=a1t1
,vAy=a1t1
粒子在A点速度方向与竖直线PQ夹角为30°。
解得:![]() ,
,![]()
由几何关系得:ysin60°-xcos60°=d,
解得:![]() ,
,![]()
由牛顿第二定律得:qE1=ma1,
解得:![]()
设粒子从A到B运动过程中,加速度大小为a2,历时t2,
水平方向上有:vAsin30°=![]() a2sin60°,
a2sin60°,![]() ,qE2=ma2,
,qE2=ma2,
解得:![]() ,
,![]() ;
;
(3) 分析知:粒子过A点后,速度方向恰与电场E2方向垂直,再做类平抛运动,
粒子到达B点时动能:EkB=![]() ,vB2=(2v0)2+(a2t2)2,
,vB2=(2v0)2+(a2t2)2,
解得:![]() 。
。