题目内容
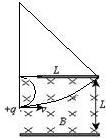
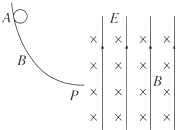
长为L的水平极板间,有垂直纸面向里的匀强磁场,如图所示,磁感应强度为B,板间距离也为L,板不带电,现有质量为m、电量为q的正电粒子(不计重力),从左边极板间中点处垂直磁感线以初速度v水平射入磁场,欲使粒子不打在极板上,求初速度v的范围.


如图所示:
由题意知,带正电的粒子从左边射出磁场,其在磁场中圆周运动的半径R<
;
因为粒子在磁场中做圆周运动洛伦兹力提供向心力即:
qvB=m
可得粒子做圆周运动的半径:
R=
粒子从左边射出,则:
<
,即v<
带正电的粒子不从右边射出,如图所示,此时粒子的最大半径为R,由上图可知:
R2=L2+(R-
)2
可得粒子圆周运动的最大半径:
R=
又因为粒子做圆周运动,洛伦兹力提供向心力,粒子不从右边射出,则:
>
即此时v>
所以粒子不从磁场区域射出速度满足:v<
或者v>
.
答:初速度v的范围:v>
或v<
.
由题意知,带正电的粒子从左边射出磁场,其在磁场中圆周运动的半径R<
| L |
| 4 |
因为粒子在磁场中做圆周运动洛伦兹力提供向心力即:
qvB=m
| v2 |
| R |
可得粒子做圆周运动的半径:
R=
| mv |
| qB |
粒子从左边射出,则:
| mv |
| qB |
| L |
| 4 |
| qBL |
| 4m |
带正电的粒子不从右边射出,如图所示,此时粒子的最大半径为R,由上图可知:
R2=L2+(R-
| L |
| 2 |
可得粒子圆周运动的最大半径:
R=
| 5L |
| 4 |
又因为粒子做圆周运动,洛伦兹力提供向心力,粒子不从右边射出,则:
| mv |
| qB |
| 5L |
| 4 |
即此时v>
| 5qBL |
| 4m |
所以粒子不从磁场区域射出速度满足:v<
| qBL |
| 4m |
| 5qBL |
| 4m |
答:初速度v的范围:v>
| 5qBL |
| 4m |
| qBL |
| 4m |


练习册系列答案
相关题目
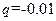 C的质点,只受到重力、电场力和空气阻力三个力作用,由空中的a点运动到b点,重力势能增加3J,克服空气阻力做功0.5J,机械能增加0.5J,则下列判断正确的是
C的质点,只受到重力、电场力和空气阻力三个力作用,由空中的a点运动到b点,重力势能增加3J,克服空气阻力做功0.5J,机械能增加0.5J,则下列判断正确的是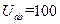 V
V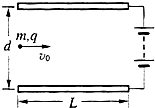



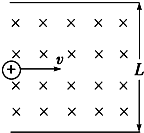
 的变化图像如图15-2图所示,电压的最大值为U0、周期为T0,在两极板外有垂直纸面向里的匀强磁场。若将一质量为m0、电荷量为q的带正电的粒子从板内a孔处静止释放,经电场加速后进入磁场,在磁场中运动时间T0后恰能再次从a 孔进入电场加速。现该粒子的质量增加了
的变化图像如图15-2图所示,电压的最大值为U0、周期为T0,在两极板外有垂直纸面向里的匀强磁场。若将一质量为m0、电荷量为q的带正电的粒子从板内a孔处静止释放,经电场加速后进入磁场,在磁场中运动时间T0后恰能再次从a 孔进入电场加速。现该粒子的质量增加了 。(粒子在两极板间的运动时间不计,两极板外无电场,不考虑粒子所受的重力)
。(粒子在两极板间的运动时间不计,两极板外无电场,不考虑粒子所受的重力)