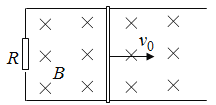
题目内容
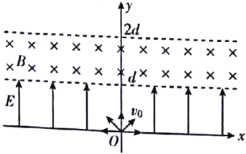
【题目】如图所示,在![]() 轴右侧平面内存在方向垂直面向里的匀强磁场,磁感应强度大小
轴右侧平面内存在方向垂直面向里的匀强磁场,磁感应强度大小![]() ,坐标原点
,坐标原点![]() 有一放射源,可以向
有一放射源,可以向![]() 轴右侧平面沿各个方向6放射比荷为
轴右侧平面沿各个方向6放射比荷为![]() 的正离子,这些离子速率分别在从0到最大值
的正离子,这些离子速率分别在从0到最大值![]() 的范围内,不计离子之间的相互作用.
的范围内,不计离子之间的相互作用.
(1)求离子打到![]() 轴上的范围;
轴上的范围;
(2)若在某时刻沿![]() 方向放射各种速率的离子,求经过
方向放射各种速率的离子,求经过![]() 时这些离子所在位置构成的曲线方程;
时这些离子所在位置构成的曲线方程;
(3)若从某时刻开始向![]() 轴右侧各个方向放射各种速率的离子,求经过
轴右侧各个方向放射各种速率的离子,求经过![]() 时已进入磁场的离子可能出现的区域面积.
时已进入磁场的离子可能出现的区域面积.
【答案】(1)离子打到![]() 轴上的范围为0到
轴上的范围为0到![]() ;(2)
;(2) ;(3)
;(3)
【解析】
(1)离子进入磁场中做圆周运动的最大半径为![]() ,由牛顿第二定律得:
,由牛顿第二定律得:
![]()
解得:
![]()
由几何关系知,离子打到![]() 轴上的范围为0到
轴上的范围为0到![]() 。
。
(2)离子在磁场中运动的周期为![]() ,则
,则
![]()
经过时间![]() 这些离子轨迹所对应的圆心角为
这些离子轨迹所对应的圆心角为![]() ,则
,则
![]()
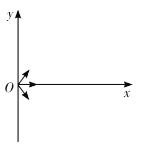
这些离子构成的曲线如图1所示,并令某一离子在此时刻的坐标为![]() ,则
,则
![]()
![]()
代入数据并化简得:


甲 乙
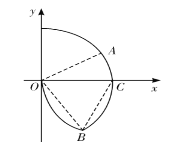
(3)将第(2)问中图1的![]() 段从沿
段从沿![]() 轴方向顺时针方向旋转,在
轴方向顺时针方向旋转,在![]() 轴上找一点
轴上找一点![]() ,以
,以![]() 为半径作圆弧,相交于
为半径作圆弧,相交于![]() ,则两圆弧及
,则两圆弧及![]() 轴所围成的面积即为在
轴所围成的面积即为在![]() 向
向![]() 轴右侧各个方向不断放射各种速度的离子在
轴右侧各个方向不断放射各种速度的离子在![]() 时已进入磁场的离子所在区域,如图2所示。
时已进入磁场的离子所在区域,如图2所示。
由几何关系可求得此面积为:
![]()
则:


练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目