题目内容
 (2009?深圳一模)一根长为l的线吊着一质量为m的带电量为q的小球静止在水平向右的匀强电场中,如图所示,线与竖直方向成37°角,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响,(重力加速度为g),求:
(2009?深圳一模)一根长为l的线吊着一质量为m的带电量为q的小球静止在水平向右的匀强电场中,如图所示,线与竖直方向成37°角,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响,(重力加速度为g),求:(1)匀强电场的电场强度的大小;
(2)求小球经过最低点时线的拉力.
分析:(1)小球静止时在竖直线的右边,根据小球静止时受平衡力,可以判断出小球的受力的方向向右,与电场线的方向相同,因此小球带正电;对小球进行受力分析,水平方向和竖直方向的受力都平衡,即可得解;
(2)水平方向不受力了,平衡破坏了,小球在竖直向下的重力和竖直向上的电场力的作用下,在绳子的约束下,在竖直平面内沿圆弧摆下,做圆周运动,或沿圆弧来回运动,根据动能定理,带电小球到最低点时重力和电场力做的功全部转化为小球的动能,此时速度最大,列式即可得解.
(2)水平方向不受力了,平衡破坏了,小球在竖直向下的重力和竖直向上的电场力的作用下,在绳子的约束下,在竖直平面内沿圆弧摆下,做圆周运动,或沿圆弧来回运动,根据动能定理,带电小球到最低点时重力和电场力做的功全部转化为小球的动能,此时速度最大,列式即可得解.
解答:解::(1)小球平衡时受到绳子的拉力、重力和电场力,
由平衡条件得:mgtan37°=qE
解得:E=
(2)电场方向变成向下后,重力和电场力都向下,
 两个力做功,小球开始摆动做圆周运动
两个力做功,小球开始摆动做圆周运动
由动能定理:
mv2=(mg+qE)L(1-cos37°)
在最低点时绳子的拉力、重力和电场力的合力提供向心力,T-(mg+qE)=m
解得:T=(mg+qE)+m
=
答:(1)匀强电场的电场强度E=
;
(2)
mg.

由平衡条件得:mgtan37°=qE
解得:E=
| 3mg |
| 4q |
(2)电场方向变成向下后,重力和电场力都向下,
 两个力做功,小球开始摆动做圆周运动
两个力做功,小球开始摆动做圆周运动由动能定理:
| 1 |
| 2 |
在最低点时绳子的拉力、重力和电场力的合力提供向心力,T-(mg+qE)=m
| v2 |
| L |
解得:T=(mg+qE)+m
| V2 |
| L |
| 49mg |
| 20 |
答:(1)匀强电场的电场强度E=
| 3mg |
| 4q |
(2)
| 49 |
| 20 |
点评:(1)掌握力的合成和分解,运用共点力平衡的条件找出力与力的关系.(2)带电粒子在复合场中的圆周运动一般由动力学公式求解,一般的曲线运动一般由动能定理求解.

练习册系列答案
相关题目
 (2009?深圳一模)在光滑水平面上有两个小木块A和B,其质量mA=1kg、mB=4kg,它们中间用一根轻质弹簧相连.一颗水平飞行的子弹质量为m=50g,以V0=500m/s的速度在极短时间内射穿两木块,已知射穿A木块后子弹的速度变为原来的
(2009?深圳一模)在光滑水平面上有两个小木块A和B,其质量mA=1kg、mB=4kg,它们中间用一根轻质弹簧相连.一颗水平飞行的子弹质量为m=50g,以V0=500m/s的速度在极短时间内射穿两木块,已知射穿A木块后子弹的速度变为原来的 (2009?深圳一模)如图所示,匀强磁场的方向竖直向下.磁场中有光滑的水平桌面,在桌面上平放着内壁光滑、底部有带电小球的试管.试管在水平拉力F作用下向右匀速运动,带电小球能从管口处飞出.关于带电小球及其在离开试管前的运动,下列说法中正确的是( )
(2009?深圳一模)如图所示,匀强磁场的方向竖直向下.磁场中有光滑的水平桌面,在桌面上平放着内壁光滑、底部有带电小球的试管.试管在水平拉力F作用下向右匀速运动,带电小球能从管口处飞出.关于带电小球及其在离开试管前的运动,下列说法中正确的是( )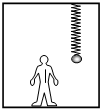 (2009?深圳一模)如图所示,轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小铁球,在电梯运行时,乘客发现弹簧的伸长量比电梯静止时的伸长量小,这一现象表明此过程中( )
(2009?深圳一模)如图所示,轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小铁球,在电梯运行时,乘客发现弹簧的伸长量比电梯静止时的伸长量小,这一现象表明此过程中( )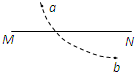 (2009?深圳一模)如图所示,MN是一负点电荷产生的电场中的一条电场线.一个带正电的粒子(不计重力)从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( )
(2009?深圳一模)如图所示,MN是一负点电荷产生的电场中的一条电场线.一个带正电的粒子(不计重力)从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( )