题目内容
如图所示光滑水平固定的桌面上静止一质量m1=5Kg的物块A。物块距桌边缘的距离为6m。桌的右边紧临边缘有一水平放置的与桌等高的传送带。传送带上有一质量为m2=2Kg的物块B随传送带一起以2m/s的速度向左匀速运动。现给A施以水平向右的大小为6M的作用力并持续3s撤去。当A刚离开平台时恰与B 发生碰撞且粘在了一起。设碰撞时间极短,传送带长度为1.8m。两物块与传送带的动磨擦因数均为0.1,求物块能否向右离开传送带?若能离开传送带,求离开时的速度。(g取10m/s2)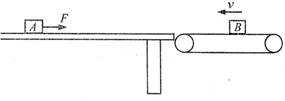
已知A到桌右边缘的距离为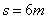 ,水平作用力
,水平作用力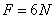 ,A的质量为
,A的质量为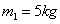 ,力F的作用时间为
,力F的作用时间为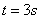 ,则A产生的加速度为
,则A产生的加速度为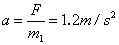 (2分)
(2分)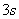 内的位移为
内的位移为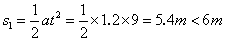 (2分)所以离开桌子边缘时的速度为
(2分)所以离开桌子边缘时的速度为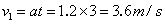 (2分)A与B相撞前后动量守恒,碰后的共同速度为
(2分)A与B相撞前后动量守恒,碰后的共同速度为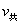 ,则
,则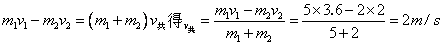 (6分)假设物块刚离开传送带时其速度为零,位移
(6分)假设物块刚离开传送带时其速度为零,位移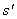 ,则
,则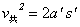 加速度为
加速度为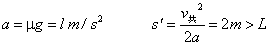 (4分)所以物块能离开传送带,设离开传送带时的速度为
(4分)所以物块能离开传送带,设离开传送带时的速度为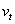 ,于是有:
,于是有: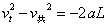
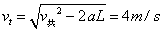 (4分)
(4分)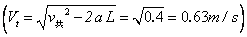

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图所示,水平固定倾角为30°的光滑斜面上有两质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向左推力F使A、B均静止在斜面上,此时弹簧的长度为l,则弹簧原长和推力F的大小分别为( )
如图所示,水平固定倾角为30°的光滑斜面上有两质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向左推力F使A、B均静止在斜面上,此时弹簧的长度为l,则弹簧原长和推力F的大小分别为( )A、l+
| ||||||
B、l-
| ||||||
C、1+
| ||||||
D、l-
|
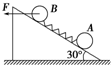 如图所示,水平固定倾角为30°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向左的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则弹簧原长和推力F的大小分别为( )
如图所示,水平固定倾角为30°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向左的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则弹簧原长和推力F的大小分别为( )A、
| ||||
B、l-
| ||||
C、l+
| ||||
D、2
|
 (2011?绍兴二模)如图所示,水平固定倾角为30°的光滑斜面上有两质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右推力F使A、B均静止在斜面上,此时弹簧的长度为l,则弹簧原长和推力为F的大小分别为( )
(2011?绍兴二模)如图所示,水平固定倾角为30°的光滑斜面上有两质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右推力F使A、B均静止在斜面上,此时弹簧的长度为l,则弹簧原长和推力为F的大小分别为( )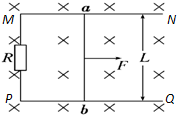 如图所示,水平固定放置的两根平行光滑导轨MN、PQ,两导轨间距L=0.50m,导轨间接有电阻R=0.50Ω.一导体棒ab垂直跨放在导轨上,现在力F的作用下在导轨上匀速滑动.已知除电阻R外,导体棒ab和导轨的电阻都可忽略不计,匀强磁场垂直框架平面向里,磁感应强度B=0.40T.导轨足够长.当ab以v=4.0m/s的速度向右匀速滑动时,(g=10m/s2)求:
如图所示,水平固定放置的两根平行光滑导轨MN、PQ,两导轨间距L=0.50m,导轨间接有电阻R=0.50Ω.一导体棒ab垂直跨放在导轨上,现在力F的作用下在导轨上匀速滑动.已知除电阻R外,导体棒ab和导轨的电阻都可忽略不计,匀强磁场垂直框架平面向里,磁感应强度B=0.40T.导轨足够长.当ab以v=4.0m/s的速度向右匀速滑动时,(g=10m/s2)求: