Question

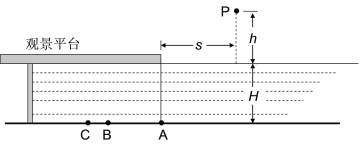
【题目】某公园的湖面上有一伸向水面的观景台，截面图如图所示，观景台下表面恰好和水面相平，A为观景台右侧面在湖底的投影，水深H=8m．在距观景台右侧面s=4m处有一可沿竖直方向移动的单色点光源P，现该光源从距水面高h=3m处向下移动动 接近水面的过程中，观景台水下部分被照亮，最近距离为AB，若AB=6m，求：

①水的折射率n；

②求最远距离AC(计算结果可以保留根号)．

Answer 1

【答案】(1) （2）

【解析】试题观景台水下被照亮的最近距离为AB，光线在水面发生了折射，由数学知识求入射角与折射角的正弦值，即可求得折射率；点光源S接近水面时，入射角为90°，光能照亮的距离最远，由折射定律求出折射角，即可由几何知识求解最远距离AC。

（1）从P点射向O点的光经水平面折射后射向B点，

根据几何关系可得：

根据折射率可得：

（2）从点射向O点的光经O点折射后射向C点，此时入射角达到最大，最大接近900，则∠AOC=C，临界角为：

解得：