题目内容
13.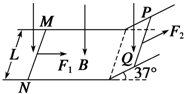 如图所示,两条平行的金属导轨相距L=1m,金属导轨的倾斜部分与水平方向的夹角为37°,整个装置处在竖直向下的匀强磁场中.金属棒MN和PQ的质量均为m=0.2kg,电阻分别为RMN=1Ω和RPQ=2Ω.MN置于水平导轨上,与水平导轨间的动摩擦因数μ=0.5,PQ置于光滑的倾斜导轨上,两根金属棒均与导轨垂直且接触良好.从t=0时刻起,MN棒在水平外力F1的作用下由静止开始以a=1m/s2的加速度向右做匀加速直线运动,PQ则在平行于斜面方向的力F2作用下保持静止状态.t=3s时,PQ棒消耗的电功率为8W,不计导轨的电阻,水平导轨足够长,MN始终在水平导轨上运动.求:
如图所示,两条平行的金属导轨相距L=1m,金属导轨的倾斜部分与水平方向的夹角为37°,整个装置处在竖直向下的匀强磁场中.金属棒MN和PQ的质量均为m=0.2kg,电阻分别为RMN=1Ω和RPQ=2Ω.MN置于水平导轨上,与水平导轨间的动摩擦因数μ=0.5,PQ置于光滑的倾斜导轨上,两根金属棒均与导轨垂直且接触良好.从t=0时刻起,MN棒在水平外力F1的作用下由静止开始以a=1m/s2的加速度向右做匀加速直线运动,PQ则在平行于斜面方向的力F2作用下保持静止状态.t=3s时,PQ棒消耗的电功率为8W,不计导轨的电阻,水平导轨足够长,MN始终在水平导轨上运动.求:(1)磁感应强度B的大小;
(2)0~3s时间内通过MN棒的电荷量;
(3)求t=6s时F2的大小和方向;
(4)若改变F1的作用规律,使MN棒的运动速度v与位移x满足关系:v=0.4x,PQ棒仍然静止在倾斜轨道上.求MN棒从静止开始到x=5m的过程中,系统产生的焦耳量.
分析 (1)t=3s时,PQ棒消耗的电功率为8W,由功率公式P=I2R可求出电路中电流,由闭合电路欧姆定律求出感应电动势.已知MN棒做匀加速直线运动,由速度时间公式求出t=3s时的速度,即可由公式E=BLv求出磁感应强度B;
(2)根据法拉第电磁感应定律、欧姆定律和电量公式推导出感应电荷量的表达式q=$\frac{△Φ}{{R}_{总}}$,代入数据可求得通过MN棒的电荷量;
(3)根据速度公式v=at、感应电动势公式E=BLv、闭合电路欧姆定律、安培力公式F=BIL结合,可求出PQ棒所受的安培力大小,再由平衡条件求解F2的大小和方向;
(4)改变F1的作用规律时,MN棒做变加速直线运动,因为速度v与位移s成正比,所以电流I、安培力也与位移s成正比,可根据安培力的平均值求出安培力做功,系统产生的热量等于克服安培力,即可得解.
解答 解:(1)当t=3 s时,设MN的速度为v1.
当t=3s时,PQ棒消耗的电功率为8W,则有:P=I2RPQ;
得:I=2A
MN棒做匀加速直线运动,t1=3s时速度为:v1=at=3 m/s
此时MN棒将产生感应电动势为:E1=BLv1
由闭合电路欧姆定律得:E1=I(RMN+RPQ)
代入数据得:B=2 T.
(2)t1=3s时MN棒通过的位移为:x=$\frac{1}{2}a{t}_{1}^{2}$=$\frac{1}{2}×1×{3}^{2}$m=4.5m
回路磁通量的变化量为:△Φ=BLx=2×1×4.5Wb=9W
根据法拉第电磁感应定律得:$\overline{E}$=$\frac{△Φ}{△t}$
通过MN棒的电荷量为:q=$\overline{I}$△t=$\frac{\overline{E}}{{R}_{MN}+{R}_{PQ}}$△t=$\frac{△Φ}{{R}_{MN}+{R}_{PQ}}$
代入数据可得:q=3 C
(3)当t=6 s时,设MN的速度为v2,则有:
v2=at=6 m/s
感应电动势为:E2=BLv2=12 V
感应电流为:I2=$\frac{{E}_{2}}{{R}_{MN}+{R}_{PQ}}$=4 A
PQ棒所受的安培力为:F安=BI2L=8 N
规定沿斜面向上为正方向,对PQ进行受力分析可得:
F2+F安cos 37°=mgsin 37°
代入数据:F2=-5.2 N(负号说明力的方向沿斜面向下)
(4)MN棒做变加速直线运动,当x=5 m时,v=0.4x=0.4×5 m/s=2 m/s
因为速度v与位移x成正比,所以电流I、安培力也与位移x成正比,安培力做功为:
W安=-$\frac{1}{2}$BL•$\frac{BLv}{{R}_{MN}+{R}_{PQ}}$•x=-$\frac{20}{3}$ J
故系统产生的焦耳热为:
Q=-W安=$\frac{20}{3}$ J.
答:(1)磁感应强度B的大小是2T;
(2)0~3s时间内通过MN棒的电荷量为3C;
(3)t=6s时F2的大小为5.2N,方向沿斜面向下;
(4)MN棒从静止开始到s=5m的过程中,系统产生的热量为$\frac{20}{3}$J.
点评 本题是双杆类型,分别研究它们的情况是解答的基础,运用力学和电路、电磁感应的规律研究MN棒,其中对于感应电荷量,要熟悉一般表达式q=n$\frac{△Φ}{{R}_{总}}$,知道△φ与棒的位移有关.本题关键要抓住安培力与位移是线性关系,安培力的平均值等于初末时刻的平均值,从而可求出安培力做功.

| A. | 刷牙时,牙刷与牙齿之间的摩擦 | |
| B. | 自行车刹车时,刹车皮与轮圈之间的摩擦 | |
| C. | “神舟5号”载人飞船升空时,飞船与空气的摩擦 | |
| D. | 手拿物体时,手与物体之间的摩擦 |
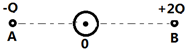
| A. | 球壳上的感应电荷在0点的场强为0 | |
| B. | 球壳上的感应电荷在0点的场强大小为$\frac{3kQ}{L^2}$ | |
| C. | 0点的场强为0 | |
| D. | 0点的场强大小为$\frac{3kQ}{L^2}$ |

| A. | 瞬时速度 | B. | 速率 | C. | 平均速度 | D. | 路程与时间的比 |
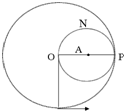 一轻绳系住一质量为m的小球悬挂在O点,在最低点给小球一水平初速度,小球恰能在竖直平面内绕O点做圆周运动,若在水平半径OP的中点A处钉一枚光滑的钉子,仍在最低点给小球同样的初速度,则小球向上通过P点后将绕A点做圆周运动,则到达最高点N时,绳子的拉力大小为( )
一轻绳系住一质量为m的小球悬挂在O点,在最低点给小球一水平初速度,小球恰能在竖直平面内绕O点做圆周运动,若在水平半径OP的中点A处钉一枚光滑的钉子,仍在最低点给小球同样的初速度,则小球向上通过P点后将绕A点做圆周运动,则到达最高点N时,绳子的拉力大小为( )| A. | mg | B. | 2mg | C. | 3mg | D. | 4mg |
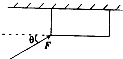 如图所示,质量为m的物体在恒力F作用下沿天花板做匀速直线运动,物体与天花板间动摩擦因数为μ,则物体受到摩镲力大小为( )
如图所示,质量为m的物体在恒力F作用下沿天花板做匀速直线运动,物体与天花板间动摩擦因数为μ,则物体受到摩镲力大小为( )| A. | Fsinθ | B. | Fcosθ | C. | μmg | D. | μ(mg-Fsinθ) |
 在静电学中有如下结论:一个完整的半径为R的均匀带电球壳,如果其带电量为Q,则其内部任意一点的电势均为φ=k$\frac{Q}{R}$.如图,有一个均匀带正电的半球壳,带电量为q,o为球心,P、Q 为关于o对称的两个位置,已知P点的电势为φp,则Q点的电势为2k$\frac{Q}{R}$-φp.
在静电学中有如下结论:一个完整的半径为R的均匀带电球壳,如果其带电量为Q,则其内部任意一点的电势均为φ=k$\frac{Q}{R}$.如图,有一个均匀带正电的半球壳,带电量为q,o为球心,P、Q 为关于o对称的两个位置,已知P点的电势为φp,则Q点的电势为2k$\frac{Q}{R}$-φp.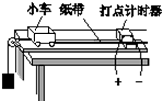 某学生在做“用打点计时器测速度”的实验时,实验装置安装完毕,小车开始运动前情景如左图所示,其中的错误之处是打点计时器使用的是直流电源,不妥之处是小车未紧靠打点计时器.
某学生在做“用打点计时器测速度”的实验时,实验装置安装完毕,小车开始运动前情景如左图所示,其中的错误之处是打点计时器使用的是直流电源,不妥之处是小车未紧靠打点计时器.