题目内容
【题目】如图所示,半径为R=0.25m的![]() 竖直圆弧轨道与平板组合成一体,其质量为M=4 kg,一轻质弹簧右端固定在平板上,弹簧的原长正好等于平板的长度。组合体放在水平地面上,并与左侧竖直墙壁紧挨在一起。将质量为m=1 kg的物块(可视为质点)从圆弧轨道上端以初速度v0=2 m/s滑入轨道,物块到达圆轨道最低点时将与弹簧接触并压缩弹簧。设小物块与平板间的摩擦因数为
竖直圆弧轨道与平板组合成一体,其质量为M=4 kg,一轻质弹簧右端固定在平板上,弹簧的原长正好等于平板的长度。组合体放在水平地面上,并与左侧竖直墙壁紧挨在一起。将质量为m=1 kg的物块(可视为质点)从圆弧轨道上端以初速度v0=2 m/s滑入轨道,物块到达圆轨道最低点时将与弹簧接触并压缩弹簧。设小物块与平板间的摩擦因数为![]() =0.2,弹簧的最大压缩量为x=0.2 m,其他接触面间的摩擦均不计,重力加速度g取10 m/s2。求:
=0.2,弹簧的最大压缩量为x=0.2 m,其他接触面间的摩擦均不计,重力加速度g取10 m/s2。求:
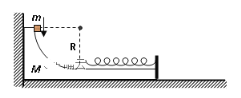
(1)小物块到达圆轨道最低点时所受的支持力;
(2)弹簧的最大弹性势能。
【答案】(1)46N(2)3.2J
【解析】
(1)设物块到达圆轨道最低点时的速度为v
![]() mv02+mgR=
mv02+mgR=![]() mv2
mv2
解得:v=3m/s
FN-mg=m![]()
解得:FN=46N
(2)设物块压缩弹簧到最大位移时共同速度为v′
mv=(m+M)v′
v′=0.6m/s
设弹簧的最大弹性势能为EP
![]() mv2=
mv2=![]() (m+M)v′2+EP+μmgx
(m+M)v′2+EP+μmgx
解得:EP=3.2J

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目