题目内容
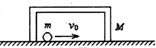 如图所示,有一光滑钢球质量为m,被一U形框扣在里面,框的质量为M,它们搁置于光滑水平面上,现让小球以速度v0向右去第一次撞击静止的框,设碰撞无机械能损失,经多次相互撞击,下面结论正确的是( )
如图所示,有一光滑钢球质量为m,被一U形框扣在里面,框的质量为M,它们搁置于光滑水平面上,现让小球以速度v0向右去第一次撞击静止的框,设碰撞无机械能损失,经多次相互撞击,下面结论正确的是( )分析:小球以速度v0向右去第一次撞击静止的框,经多次相互撞击,系统动量守恒.碰撞无机械能损失,机械能守恒.
两者结合解决问题.
两者结合解决问题.
解答:解:小球以速度v0向右去第一次撞击静止的框,系统动量守恒,能量守恒.
由于M>m,小球碰后速度向左,框的速度向右,
再过一段时间,小球与框的左侧发生碰撞,系统动量守恒,能量守恒.
小球的速度才会再次等于v0,框也重现静止状态.后面发生的情况就会重复开始得状态.
所以它们发生偶数次碰撞后,小球的速度将会再次等于v0,框也重现静止状态,与M、m数值大小关系无关,
它们发生奇数次碰撞后,小球的速度向左,框的速度向右,
故选D.
由于M>m,小球碰后速度向左,框的速度向右,
再过一段时间,小球与框的左侧发生碰撞,系统动量守恒,能量守恒.
小球的速度才会再次等于v0,框也重现静止状态.后面发生的情况就会重复开始得状态.
所以它们发生偶数次碰撞后,小球的速度将会再次等于v0,框也重现静止状态,与M、m数值大小关系无关,
它们发生奇数次碰撞后,小球的速度向左,框的速度向右,
故选D.
点评:本题考查了动量守恒定律的直接应用,要注意分两种情况进行讨论,难度适中.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 B.如图所示,在光滑的水平面上有一长L=1m的钢槽A,槽中有一物体B,A和B的质量相同,AB间的动摩擦因数μ=0.05.开始时B位于钢槽的中央,都处于静止状态.现给一个瞬时速度υ0=5m/s,使它向右运动.如果B与A两侧的挡板相碰撞是无动能损耗,则B与A的左右两挡板最多能相碰
B.如图所示,在光滑的水平面上有一长L=1m的钢槽A,槽中有一物体B,A和B的质量相同,AB间的动摩擦因数μ=0.05.开始时B位于钢槽的中央,都处于静止状态.现给一个瞬时速度υ0=5m/s,使它向右运动.如果B与A两侧的挡板相碰撞是无动能损耗,则B与A的左右两挡板最多能相碰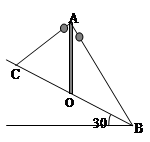
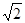 s和 2s C.
s和 2s C.
 s C.1s D.4s
s C.1s D.4s 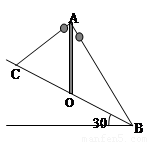
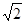 s和 2s C.
s和 2s C.