题目内容
12. 如图所示,河水的流速为4m/s,一条船要从河的南岸A点沿与河岸成30°角的直线航行到北岸下游某处,则( )
如图所示,河水的流速为4m/s,一条船要从河的南岸A点沿与河岸成30°角的直线航行到北岸下游某处,则( )| A. | 船的航行速度最小为2 m/s | |
| B. | 船的航行速度最小为3 m/s | |
| C. | 船的航行速度最小时船头指向上游与南岸成60° | |
| D. | 船的航行速度最小时船头指向下游与南岸成30° |
分析 已知合速度的方向以及一分速度的方向(水流速),根据平行四边形定则确定另一分速度(静水速)的最小值.
解答 解:根据平行四边形定则知,因为垂线段最短,所以当静水速与合速度方向垂直时,静水速最小,为:
${v}_{min}={v}_{水}sin30°=4×\frac{1}{2}m/s=2m/s$.
由图可知,船的航行速度最小时船头指向上游与南岸成60°
故AC正确,B、D错误.
故选:AC.
点评 解决本题的关键会根据平行四边形定则对速度进行合成,以及在知道合速度方向和一分速度大小方向的情况下,能够求出另一分速度的最小值.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
13.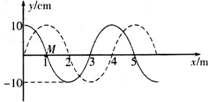 如图所示,实线是一列简谐横波在t时刻的波形图,虚线是在t时刻后△t=0.2s时刻的波形图.已知△t<T,若该简谐波的波速为5m/s,则( )
如图所示,实线是一列简谐横波在t时刻的波形图,虚线是在t时刻后△t=0.2s时刻的波形图.已知△t<T,若该简谐波的波速为5m/s,则( )
 如图所示,实线是一列简谐横波在t时刻的波形图,虚线是在t时刻后△t=0.2s时刻的波形图.已知△t<T,若该简谐波的波速为5m/s,则( )
如图所示,实线是一列简谐横波在t时刻的波形图,虚线是在t时刻后△t=0.2s时刻的波形图.已知△t<T,若该简谐波的波速为5m/s,则( )| A. | 质点M在t时刻的振动方向为y轴正方向 | |
| B. | 质点M在△t时刻的振动方向为y轴负方向 | |
| C. | 质点M在△t时间内通过的路程为0.1m | |
| D. | 质点M在时间内通过的路程为0.3m |
14.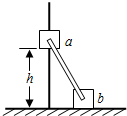 如图,滑块a、b的质量均为m,a套在固定竖直杆上,与光滑水平地面相距h,b放在地面上,a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点,重力加速度大小为g.则( )
如图,滑块a、b的质量均为m,a套在固定竖直杆上,与光滑水平地面相距h,b放在地面上,a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点,重力加速度大小为g.则( )
 如图,滑块a、b的质量均为m,a套在固定竖直杆上,与光滑水平地面相距h,b放在地面上,a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点,重力加速度大小为g.则( )
如图,滑块a、b的质量均为m,a套在固定竖直杆上,与光滑水平地面相距h,b放在地面上,a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点,重力加速度大小为g.则( )| A. | a落地前,轻杆对b一直做正功 | |
| B. | a落地时速度大小为$\sqrt{2gh}$ | |
| C. | a下落过程中,其加速度大小始终不大于g | |
| D. | a落地前,当a的机械能最小时,b对地面的压力大小为mg |
7. 图甲为远距离输电示意图,升压变压器原、副线圈匝数比为1:100,降压变压器原、副线圈匝数之比为100:1,远距离输电线的总电阻为100Ω.若升压变压器的输入电压如乙所示,输入功率为500kW,计算出用户端电压为( )
图甲为远距离输电示意图,升压变压器原、副线圈匝数比为1:100,降压变压器原、副线圈匝数之比为100:1,远距离输电线的总电阻为100Ω.若升压变压器的输入电压如乙所示,输入功率为500kW,计算出用户端电压为( )
 图甲为远距离输电示意图,升压变压器原、副线圈匝数比为1:100,降压变压器原、副线圈匝数之比为100:1,远距离输电线的总电阻为100Ω.若升压变压器的输入电压如乙所示,输入功率为500kW,计算出用户端电压为( )
图甲为远距离输电示意图,升压变压器原、副线圈匝数比为1:100,降压变压器原、副线圈匝数之比为100:1,远距离输电线的总电阻为100Ω.若升压变压器的输入电压如乙所示,输入功率为500kW,计算出用户端电压为( )| A. | 250V | B. | 220V | C. | 230V | D. | 200V |
4.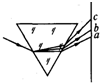 如图所示,一细束白光通过三棱镜折射后分为各种单色光,取其中a、b、c三种单色光,并同时做如下实验:①让这三种单色光分别通过同一双缝干涉装置在光屏上产生干涉条纹(双缝间距和缝屏间距不变);②让这三种单色光分别照射锌板;③让这三种单色光分别垂直投射到一条直光纤的端面上;下列说法中正确的是( )
如图所示,一细束白光通过三棱镜折射后分为各种单色光,取其中a、b、c三种单色光,并同时做如下实验:①让这三种单色光分别通过同一双缝干涉装置在光屏上产生干涉条纹(双缝间距和缝屏间距不变);②让这三种单色光分别照射锌板;③让这三种单色光分别垂直投射到一条直光纤的端面上;下列说法中正确的是( )
 如图所示,一细束白光通过三棱镜折射后分为各种单色光,取其中a、b、c三种单色光,并同时做如下实验:①让这三种单色光分别通过同一双缝干涉装置在光屏上产生干涉条纹(双缝间距和缝屏间距不变);②让这三种单色光分别照射锌板;③让这三种单色光分别垂直投射到一条直光纤的端面上;下列说法中正确的是( )
如图所示,一细束白光通过三棱镜折射后分为各种单色光,取其中a、b、c三种单色光,并同时做如下实验:①让这三种单色光分别通过同一双缝干涉装置在光屏上产生干涉条纹(双缝间距和缝屏间距不变);②让这三种单色光分别照射锌板;③让这三种单色光分别垂直投射到一条直光纤的端面上;下列说法中正确的是( )| A. | 如果单色光b能产生光电效应,则单色光a一定能产生光电效应 | |
| B. | 单色光c的波动性最显著 | |
| C. | 单色光a穿过光纤的时间最长 | |
| D. | 单色光c形成的干涉条纹间距最小 |
2.一定质量的气体,从初态(p0、V0、T0)先经等压变化使温度上升到$\frac{3}{2}$T0,再经等容变化使压强减小到$\frac{1}{2}$p0,则气体最后状态为( )
| A. | $\frac{1}{2}$p0、V0、$\frac{3}{2}$T0 | B. | $\frac{1}{2}$p0、$\frac{3}{2}$V0、$\frac{3}{4}$T0 | C. | $\frac{1}{2}$p0、V0、$\frac{3}{4}$T0 | D. | $\frac{1}{2}$p0、$\frac{3}{2}$V0、T0 |
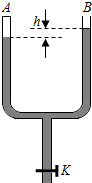 如图,一粗细均匀的U形管竖直放置,A侧上端封闭,B侧上端与大气相通,下端开口处开关K关闭,A侧空气柱的长度为l=10.0cm,B侧水银面比A侧的高h=3.0cm.现将开关K打开,从U形管中放出部分水银,当两侧水银面的高度差为h1=10.0cm时将开关K关闭.已知大气压强p0=75.0cmHg.
如图,一粗细均匀的U形管竖直放置,A侧上端封闭,B侧上端与大气相通,下端开口处开关K关闭,A侧空气柱的长度为l=10.0cm,B侧水银面比A侧的高h=3.0cm.现将开关K打开,从U形管中放出部分水银,当两侧水银面的高度差为h1=10.0cm时将开关K关闭.已知大气压强p0=75.0cmHg.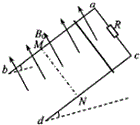 如图所示,ab、cd为间距l=1m的光滑倾斜金属导轨,与水平面的夹角为θ=30°,导轨电阻不计,ac间连接有一个R=2.4Ω的电阻,空间存在磁应强度B0=2T的匀强磁场,方向垂直于导轨平面向上,将一根金属棒放置在导轨上距ac为x0=0.5m处,金属棒的质量m=0.5kg,电阻r=0.8Ω.现将金属棒由静止释放,金属棒沿导轨向下运动的过程中始终与ac平行且与导轨接触良好.已知当金属棒向下滑行x=1.6m到达MN处时已经达到稳定速度,金属导轨足够长,g取10m/s2.则:
如图所示,ab、cd为间距l=1m的光滑倾斜金属导轨,与水平面的夹角为θ=30°,导轨电阻不计,ac间连接有一个R=2.4Ω的电阻,空间存在磁应强度B0=2T的匀强磁场,方向垂直于导轨平面向上,将一根金属棒放置在导轨上距ac为x0=0.5m处,金属棒的质量m=0.5kg,电阻r=0.8Ω.现将金属棒由静止释放,金属棒沿导轨向下运动的过程中始终与ac平行且与导轨接触良好.已知当金属棒向下滑行x=1.6m到达MN处时已经达到稳定速度,金属导轨足够长,g取10m/s2.则: 如图所示,AB是竖直平面内的$\frac{1}{4}$圆弧形光滑轨迹一端B与水平轨道相同,一个小物块自A点又静止开始沿轨道下滑.已知轨道半径R=0.2m,小物块的质量m=0.1kg,小物块与水平面间的摩擦因数μ=0.5,取g=10m/s2.求:
如图所示,AB是竖直平面内的$\frac{1}{4}$圆弧形光滑轨迹一端B与水平轨道相同,一个小物块自A点又静止开始沿轨道下滑.已知轨道半径R=0.2m,小物块的质量m=0.1kg,小物块与水平面间的摩擦因数μ=0.5,取g=10m/s2.求: