题目内容
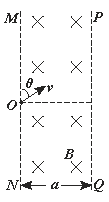
【题目】如图所示，竖直平行线MN、PQ间距离为a，其间存在垂直纸面向里的匀强磁场(含边界PQ)，磁感应强度为B，MN上O处的粒子源能沿不同方向释放比荷为
的带负电粒子，速度大小相等、方向均垂直磁场。粒子间的相互作用及重力不计。设粒子速度方向与射线OM夹角为θ ，当粒子沿θ＝60°射入时，恰好垂直PQ射出，则
A. 粒子的速率为
B. PQ边界上有粒子射出的长度为
C. 沿θ=120°射入的粒子，在磁场中运动的时间最长
D. 从PQ边界射出的粒子在磁场中运动的最短时间为
【答案】ABC
【解析】由题设条件，当粒子沿θ=60°射入时，恰好垂直PQ射出，由几何关系求出做匀速圆周运动的半径r=2a，由洛仑兹力提供向心力：qBv＝m
，从而得到：
，所以选项A正确；沿θ=120°射入的粒子由几何关系知道，其运动轨迹恰与PQ边相切，粒子从MN边射出，该粒子在磁场中偏转120°，运动时间最长，所以选项C正确；沿竖直向上射出的粒子打的位置最高，由几何关系可得
，而以θ=120°射入的粒子其轨迹与PQ相切，打的位置最低，由几何关系有：
，所以打在PQ的长度为y1+y2=2
a，所以选项B正确；要使粒子从PQ边射出时时间最短，则以a为弦长的轨迹所对应的时间最短。由几何半径知：其对应的圆心角θ满足：
，θ≠60°最短时间为：
，所以选项D错误。故选ABC.
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
