Question

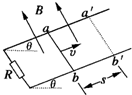如图所示，平行金属导轨与水平面间的倾角为θ，导轨电阻不计，与阻值为R的定值电阻相连，匀强磁场垂直穿过导轨平面，磁感应强度为B．有一质量为m长为l的导体棒从ab位置获得平行斜面的大小为v的初速度向上运动，最远到达a′b′的位置，滑行的距离为s，导体棒的电阻也为R，与导轨之间的动摩擦因数为μ．求
（1）上滑过程中导体棒受到的最大安培力为多少？
（2）上滑过程中导体棒克服安培力做的功为多少？
（3）上滑过程中导体棒损失的机械能为多少？

Answer 1

分析：（1）当导体棒的速度最大时，产生的感应电动势最大，感应电流最大，安培力最大，结合切割产生的感应电动势公式、闭合电路欧姆定律以及安培力的大小公式求出最大安培力的大小．
（2）对全过程运用能量守恒定律，克服安培力做功全部转化为电热．
（3）导体棒损失的机械能即为克服安培力和摩擦力做功之和，根据功能关系求出导体棒损失的机械能．

解答：解：（1）电路中总电阻为2R，感应电动势E=BLv
感应电流I=

BLv

2R

．
则最大安培力的大小F=BIL=

B2L2v

2R

；
（2）由能量守恒定律可知：导体棒动能减少的数值应该等于导体棒重力势能的增加量以及克服安培力做功产生的电热和克服摩擦阻力做功产生的内能．
其公式表示为：

1

2

mv²=mgssinθ+μmgscosθ+Q_电
Q_电热=

1

2

mv²-（mgssinθ+μmgscosθ），即为安培力做的功；
（3）根据能量守恒有

1

2

mv²=mgssinθ+μmgscosθ+Q_电
因为导体棒损失的机械能即为安培力和摩擦力做功的和，所以W_损失=

1

2

mv²-mgssinθ．
答：（1）上滑过程中导体棒受到的最大安培力为

B2L2v

2R

．
（2）上滑过程中导体棒克服安培力做的功为

1

2

mv²-（mgssinθ+μmgscosθ）．
（3）上滑过程中导体棒损失的机械能为

1

2

mv²-mgssinθ．

点评：解决本题的关键知道克服安培力做功全部转化为电热，除重力以外其它力做功等于机械能的增量，结合能量守恒定律进行求解．