题目内容
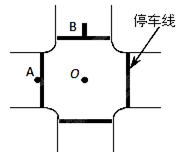
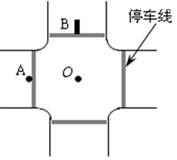
如图是一个十字路口的示意图，每条停车线到十字路中心O的距离均为20m．一人骑电动助力车以7m/s的速度到达停车线（图中A点）时，发现左前方道路一辆轿车正以8m/s的速度驶来，车头已抵达停车线（图中B），设两车均沿道路中央作直线运动，助力车可视为质点，轿车长4.8m，宽度可不计．（1）请通过计算判断两车保持上述速度匀速运动，是否会发生相撞事故？
（2）若轿车保持上述速度匀速运动，而助力车立即作匀加速直线运动，为避免发生相撞事故，助力车的加速度至少要多大？
分析：（1）通过轿车车头到达O点的时间、轿车通过O点的时间以及助力车到达O点的时间，分析是否发生相撞事故．
（2）为避免发生相撞事故，助力车到达O点的时间小于轿车车头的时间，结合位移时间公式求出最小加速度．
（2）为避免发生相撞事故，助力车到达O点的时间小于轿车车头的时间，结合位移时间公式求出最小加速度．
解答：解：（1）轿车车头到达O点的时间为 t1=
=
s=2.5s
轿车通过O点的时间为△t=
=
s=0.6s．
助力车到达O点的时间为 t2=
=
s=2.9s
因为 t1＜t2＜t1+△t，所以会发生交通事故．
（2）助力车到达O点的时间小于t1=2.5s，可避免交通事故发生，设阻力车的最小加速度为am，则
x2=v2t1+
amt12
代入数据解得am=0.8m/s2
答：（1）两车会发生相撞事故．（2）助力车的加速度至少为0.8m/s2
| x1 |
| v1 |
| 20 |
| 8 |
轿车通过O点的时间为△t=
| △x |
| v1 |
| 4.8 |
| 8 |
助力车到达O点的时间为 t2=
| x2 |
| v2 |
| 20 |
| 7 |
因为 t1＜t2＜t1+△t，所以会发生交通事故．
（2）助力车到达O点的时间小于t1=2.5s，可避免交通事故发生，设阻力车的最小加速度为am，则
x2=v2t1+
| 1 |
| 2 |
代入数据解得am=0.8m/s2
答：（1）两车会发生相撞事故．（2）助力车的加速度至少为0.8m/s2
点评：解决本题的关键掌握匀变速直线运动的运动学公式，并能灵活运用．
练习册系列答案
孟建平名校考卷系列答案
相关题目
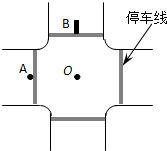如图是一个十字路口的示意图，每条停车线到十字路中心O的距离均为12m．一人骑电动助力车（可看成质点）以6m/s的速度到达停车线（图中A点）时，发现左前方道路一辆轿车正以8m/s的速度驶来，车头已抵达停车线（图中B），设两车均沿道路中央作直线运动，助力车可视为质点，轿车长4.8m，宽度可不计．
