题目内容
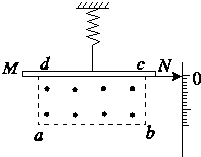一电流表的原理图如图所示．质量为m的匀质细金属棒MN的中点处通过一绝缘挂钩与一竖直悬挂的弹簧相连，弹簧劲度系数为k．在矩形区域abcd内有匀强磁场，磁感应强度大小为B，方向垂直纸面向外．与MN的右端N连接的一绝缘轻指针可指示标尺上的读数，MN的长度大于ab．当MN中没有电流通过且处于平衡状态时，MN与矩形区域的cd边重合；当MN中有电流通过时，指针示数可表示电流大小．下列说法正确的是（ ）| A、若要电流表正常工作，电流由M→N | ||
B、若将量程扩大2倍，只需将磁感应强度变为原来的
| ||
C、若将量程扩大2倍，可换一根劲度系数为原来
| ||
| D、若将量程扩大2倍，需要将磁感应强度和弹簧劲度系数均增大为原来2倍 |
分析：当电流表正常工作时，电流表有示数，金属棒将受到向下的安培力，根据左手定则可知MN中电流方向，从而确定MN的哪一端与电源正极相接．
当金属棒处于ab线上时，电流表示数最大，根据平衡条件列出受力平衡方程．扩大量程后根据推导出的平衡方程即可解出正确结果．
当金属棒处于ab线上时，电流表示数最大，根据平衡条件列出受力平衡方程．扩大量程后根据推导出的平衡方程即可解出正确结果．
解答：解：AB、为使电流表正常工作，作用于通有电流的金属棒MN的安培力必须向下．跟左手定则可知金属棒中电流从M端流向N端．故A正确；
B、没有通电流时，mg=k△x
设满量程时通过MN的电流强度为Im，则有：BLIm+mg=k（
+△x）
设量程扩大后，磁感应强度变为B′，则有：2B′LIm+mg=k（
+△x）
得：B′=
B，故B正确；
C、若换一根劲度系数为原来
倍的轻弹簧，没有通电流时：mg=k′△x′
设满量程时通过MN的电流强度为Im，则有：BLIm+mg=k′（
+△x′）
设量程扩大后，磁感应强度变为k，则有：2BLIm+mg=k′（
+△x）
得：k′=2k，故c错误；
D、由于BC的分析可得，D错误．
故选：AB．
B、没有通电流时，mg=k△x
设满量程时通过MN的电流强度为Im，则有：BLIm+mg=k（
. |
| bc |
设量程扩大后，磁感应强度变为B′，则有：2B′LIm+mg=k（
. |
| bc |
得：B′=
| 1 |
| 2 |
C、若换一根劲度系数为原来
| 1 |
| 2 |
设满量程时通过MN的电流强度为Im，则有：BLIm+mg=k′（
. |
| bc |
设量程扩大后，磁感应强度变为k，则有：2BLIm+mg=k′（
. |
| bc |
得：k′=2k，故c错误；
D、由于BC的分析可得，D错误．
故选：AB．
点评：本题重点要建立好模型，将电流表的量程，与MN的位移建立连接关系，进而由MN的位移x与弹力建立关系，最终在列平衡方程的时候，注意形变量不要用全部的，只用从cd到ab的，这样就把重力避开了．
练习册系列答案
相关题目
（2008?天津模拟）传感器是把非电学量（如速度、温度、压力等）的变化转换成电学量的变化的一种元件，在自动控制中有着相当广泛的应用．有一种测量人的体重的电子秤，其测量部分的原理图如图中的虚线框所示，它主要由压力传感器R（电阻值会随所受压力大小发生变化的可变电阻）、显示体重大小的仪表A（实质是理想的电流表）组成．压力传感器表面能承受的最大压强为1×107Pa，且已知压力传感器R的电阻与所受压力的关系如下表所示．设踏板和压杆的质量可以忽略不计，接通电源后，压力传感器两端的电压恒为4.8V，取g=10m/s2．请回答：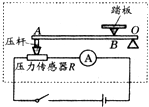
有一种测量人的体重和身高的电子秤，其测体重部分的原理图如图中的虚线框所示，它主要由三部分构成：踏板和压力杠杆ABO，压力传感器R（电阻值会随所受压力大小发生变化的可变电阻），显示体重大小的仪表A（实质是电流表）．其中
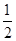倍
倍