题目内容
12. 一根放在水平面内的光滑玻璃管绝缘性能很好,管内部有两个完全一样的弹性金属小球A和B(如图所示),分别带电荷量9Q和-Q.两球从图中位置由静止释放,问两球再次经过图中位置时,A球的瞬时加速度为释放时的几倍?
一根放在水平面内的光滑玻璃管绝缘性能很好,管内部有两个完全一样的弹性金属小球A和B(如图所示),分别带电荷量9Q和-Q.两球从图中位置由静止释放,问两球再次经过图中位置时,A球的瞬时加速度为释放时的几倍?
分析 碰撞前两球带异种电荷,相互吸引而发生碰撞,碰后电量平分,根据库仑定律和牛顿第二定律研究库仑力,即可求解.
解答 解:碰撞后两球的带电量均为q=$\frac{9Q-Q}{2}$=4Q,经过图示位置时两球间距离为r,则根据库仑定律和牛顿第二定律得
碰撞前经过图示位置时:k$\frac{9Q•Q}{{r}^{2}}$=F1
碰撞后经过图示位置时:k$\frac{{(4Q)}^{2}}{{r}^{2}}$=F2,
则得F1:F2=9:16,
由F=ma可知,加速度与合力成正比,
即A球瞬时加速度为释放时的$\frac{16}{9}$倍,
答:A球瞬时加速度为释放时的$\frac{16}{9}$倍.
点评 本题关键要抓住两球经过相同位置时之间的距离不变,碰撞时由于两球相同,电量平分,根据库仑定律、牛顿第二定律和能量守恒定律进行分析.

练习册系列答案
相关题目
2.关于物体的内能,下列说法中正确的是( )
| A. | 相同质量的两种物体,升高相同的温度,内能的增量一定相同 | |
| B. | 一定质量的0℃水结成0℃冰,内能一定减少 | |
| C. | 一定质量气体的体积增大,但既不吸热也不放热,内能一定减少 | |
| D. | 相同质量的两个同种物体,运动物体的内能一定大于静止物体的内能 |
3. a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行. 已知a点电势为20V,b点电势为24V,d点电势为12V.下列正确的是( )
a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行. 已知a点电势为20V,b点电势为24V,d点电势为12V.下列正确的是( )
 a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行. 已知a点电势为20V,b点电势为24V,d点电势为12V.下列正确的是( )
a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行. 已知a点电势为20V,b点电势为24V,d点电势为12V.下列正确的是( )| A. | c点电势高于a点电势 | |
| B. | 场强的方向由b指向d | |
| C. | c点电势为16V | |
| D. | 电子从b运动到c,电场力做功为-4eV |
20. 如图所示是两个由同一地点出发,沿同一直线向同一方向运动的物体A和B的速度图象.运动过程中A?B的情况是( )
如图所示是两个由同一地点出发,沿同一直线向同一方向运动的物体A和B的速度图象.运动过程中A?B的情况是( )
 如图所示是两个由同一地点出发,沿同一直线向同一方向运动的物体A和B的速度图象.运动过程中A?B的情况是( )
如图所示是两个由同一地点出发,沿同一直线向同一方向运动的物体A和B的速度图象.运动过程中A?B的情况是( )| A. | A的速度一直比B大,B没有追上A | |
| B. | B的速度一直比A大,B追上A | |
| C. | A在t1s后改做匀速直线运动,在t2s时追上A | |
| D. | 在t2s时,A?B的瞬时速度相等,A在B的前面,尚未被B追上,但此后总是要被追上的 |
7.下面说法中错误的是( )
| A. | 在一个以点电荷Q为中心,r为半径的球面上,各处的电场强度相同 | |
| B. | 在点电荷Q的电场中的某一点,放入带电量为q的另一点电荷,则q受到的电场力为$k\frac{Qq}{r^2}$,该点的电场强度为$k\frac{Q}{r^2}$ | |
| C. | 电场强度是描述电场力的性质的物理量,它仅由电场自身决定 | |
| D. | 点电荷在电场中所受到的电场力的大小和方向,除了和电场有关外,还与该点电荷所带电量和性质有关 |
4.关于物体的重心,下列说法在正确的是( )
| A. | 均匀物体的重心必定在几何中心处 | |
| B. | 规则的几何形体其重心必定在几何中心 | |
| C. | 重心是重力的作用点必定在物体上,不可能在物体外 | |
| D. | 物体的形状改变,它的重心位置不会改变 |
1.从地面以30m/s的初速度竖直上抛一球,若不计空气阻力,g取10m/s2,则球运动到距地面25m时所经历的时间可能为( )
| A. | 1s | B. | 2s | C. | 4s | D. | 6s |
2. 如图所示,a、b、c三个质量相同的小球,a从光滑斜面顶端由静止开始自由下滑,同时b、c从同一高度分别开始自由下落和平抛.不计空气阻力,下列说法正确的是( )
如图所示,a、b、c三个质量相同的小球,a从光滑斜面顶端由静止开始自由下滑,同时b、c从同一高度分别开始自由下落和平抛.不计空气阻力,下列说法正确的是( )
 如图所示,a、b、c三个质量相同的小球,a从光滑斜面顶端由静止开始自由下滑,同时b、c从同一高度分别开始自由下落和平抛.不计空气阻力,下列说法正确的是( )
如图所示,a、b、c三个质量相同的小球,a从光滑斜面顶端由静止开始自由下滑,同时b、c从同一高度分别开始自由下落和平抛.不计空气阻力,下列说法正确的是( )| A. | 它们的重力冲量相同 | |
| B. | 它们的动量变化量大小相等 | |
| C. | 它们落地时的末动能相等 | |
| D. | 它们到达地面时重力的瞬时功率相等 |
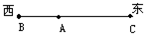 一个人从A点出发,向西走100m到达B点,然后返回向东走250m到达C点,如图所示,那么整个过程中,人的位移大小是150m,方向是从A指向C,路程是350m.
一个人从A点出发,向西走100m到达B点,然后返回向东走250m到达C点,如图所示,那么整个过程中,人的位移大小是150m,方向是从A指向C,路程是350m.