题目内容
质量为2kg的物体,在光滑水平面上受到两个水平共点力的作用,以8m/s2的加速度作匀加速直线运动,其中F1与加速度方向的夹角为30°,某时刻撤去F1,此后该物体
- A.加速度可能为5m/s2
- B.加速度可能为4m/s2
- C.加速度可能为3m/s2
- D.加速度可能为2m/s2
AB
分析:根据牛顿第二定律求出合力,F1与加速度方向的夹角为30°,根据几何知识可知,F2有最小值,求出最小值,此值即为F1撤消后,合力的最小值.根据牛顿第二定律求出加速度的取值范围.
解答:根据牛顿第二定律F合=ma=2×8N═16N
F1与加速度方向的夹角为30°,根据几何知识可知,
F2有最小值,最小值为F2m=F合sin30°=16× N=8N.
N=8N.
所以当F1,撤消后,合力的最小值为Fmin=F2m=8N,
此时合力的取值范围为8N≤F合
所以最小的加速度为amin=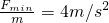 .故A、B正确,C、D错误.
.故A、B正确,C、D错误.
故选AB.
点评:解决本题的关键知道加速度的方向与合力方向相同,通过合力的大小和方向以及一个力方向得出另一个力的最小值.
分析:根据牛顿第二定律求出合力,F1与加速度方向的夹角为30°,根据几何知识可知,F2有最小值,求出最小值,此值即为F1撤消后,合力的最小值.根据牛顿第二定律求出加速度的取值范围.
解答:根据牛顿第二定律F合=ma=2×8N═16N
F1与加速度方向的夹角为30°,根据几何知识可知,
F2有最小值,最小值为F2m=F合sin30°=16×
 N=8N.
N=8N.所以当F1,撤消后,合力的最小值为Fmin=F2m=8N,
此时合力的取值范围为8N≤F合
所以最小的加速度为amin=
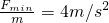 .故A、B正确,C、D错误.
.故A、B正确,C、D错误.故选AB.
点评:解决本题的关键知道加速度的方向与合力方向相同,通过合力的大小和方向以及一个力方向得出另一个力的最小值.

练习册系列答案
相关题目
质量为2kg的物体自由下落,g取10m/s2则第2s内重力的平均功率是( )
| A、400w | B、300w | C、200w | D、100w |
 如图所示,一个质量为2kg的物体静止在光滑水平面上.现沿水平方向对物体施加10N的拉力,g取10m/s2,求:
如图所示,一个质量为2kg的物体静止在光滑水平面上.现沿水平方向对物体施加10N的拉力,g取10m/s2,求: 如图所示,质量为2kg的物体与弹簧相连,弹簧的另一端固定在水平面上,物体原来处于静止状态.现用竖直向上的拉力F作用在物体上,使物体开始向上做匀加速直线运动,经0.4s弹簧刚好恢复到原长,此时物体的速度大小为2m/s,设整个过程弹簧始终在弹性限度内,取g=10m/s2.则( )
如图所示,质量为2kg的物体与弹簧相连,弹簧的另一端固定在水平面上,物体原来处于静止状态.现用竖直向上的拉力F作用在物体上,使物体开始向上做匀加速直线运动,经0.4s弹簧刚好恢复到原长,此时物体的速度大小为2m/s,设整个过程弹簧始终在弹性限度内,取g=10m/s2.则( )