题目内容
一内壁光滑的环形细圆管,位于竖直平面内,环的半径为R(比细管的半径大得多),圆管中有两个直径与细管内径相同的小球(可视为质点)。A球的质量为m1, B球的质量为m2。它们沿环形圆管顺时针运动,经过最低点时的速度都为v0。设A球运动到最低点时,球恰好运动到最高点,若要此时两球作用于圆管的合力为零,那么m1,m2,R与v0应满足关系式是。

【错解分析】错解:依题意可知在A球通过最低点时,圆管给A球向上的弹力N1为向心力,则有
 (1)
(1)B球在最高点时,圆管对它的作用力N2为m2的向心力,方向向下,则有
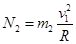 (2)
(2)因为m2由最高点到最低点机械能守恒,则有
 (3)
(3)
由式①②③解得

错解形成的主要原因是向心力的分析中缺乏规范的解题过程。没有做受力分析,导致漏掉重力,表面上看分析出了N1=N2,但实际并没有真正明白为什么圆管给m2向下的力。总之从根本上看还是解决力学问题的基本功受力分析不过关。
【正解】首先画出小球运动达到最高点和最低点的受力图,如图所示。A球在圆管最低点必受向上弹力N1,此时两球对圆管的合力为零,m2必受圆管向下的弹力N2,且N1=N2。
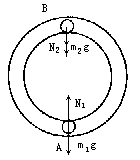
据牛顿第二定律A球在圆管的最低点有
 (1)
(1)同理m2在最高点有
 (2)
(2)m2球由最高点到最低点机械能守恒
 (3)
(3)又
 (4)
(4)由式①~④解得

【点评】比较复杂的物理过程,如能依照题意画出草图,确定好研究对象,逐一分析就会变为简单问题。找出其中的联系就能很好地解决问题。

练习册系列答案
相关题目


 ,其余的力大小和方向都不变,则质点的加速度大小为 。
,其余的力大小和方向都不变,则质点的加速度大小为 。 ,则这个推力的大小为 ( )
,则这个推力的大小为 ( ) mg
mg mg
mg mg
mg


