题目内容
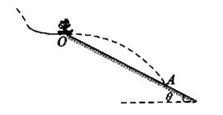
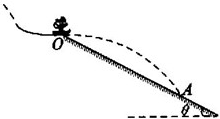 如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力,运动员可以看作质点.(sin37°=0.60,cos37°=0.80;g=10m/s2)则:
如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力,运动员可以看作质点.(sin37°=0.60,cos37°=0.80;g=10m/s2)则:(1)运动员离开O点时的速度大小为
20m/s
20m/s
;(2)运动员离斜坡的最大距离为
9m
9m
.分析:(1)运动员做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,由斜面倾角的正切等于竖直位移与水平位移之比,求解运动员离开O点时的速度大小.
(2)当运动员的速度方向与斜面平行时,运动员离斜面最远,将速度分解求出运动时间.将运动员的平抛运动分解为平行于斜面方向与垂直于斜面方向,运动员在垂直于斜面方向做初速度为v0sinθ,加速度大小为-gcosθ的匀减速运动,由位移公式求出运动员离斜坡的最大距离.
(2)当运动员的速度方向与斜面平行时,运动员离斜面最远,将速度分解求出运动时间.将运动员的平抛运动分解为平行于斜面方向与垂直于斜面方向,运动员在垂直于斜面方向做初速度为v0sinθ,加速度大小为-gcosθ的匀减速运动,由位移公式求出运动员离斜坡的最大距离.
解答:解:
(1)设运动员离开O点时的速度大小为v0.
水平位移x=v0t,竖直位移y=
gt2
又tanθ=
联立得到,v0=
=20m/s
(2)设经过时间T,运动员的速度方向与斜面平行,此时运动员离斜面最远.则
vy=v0tanθ,又vy=gT
解得 T=1.5s
将运动员的平抛运动分解为平行于斜面方向与垂直于斜面方向,运动员在垂直于斜面方向做初速度大小为v0sinθ,加速度大小为-gcosθ的匀减速运动,则得到
运动员离斜坡的最大距离S=v0sinθT-
gcosθT2=9m.
故答案为:20m/s;9m.
(1)设运动员离开O点时的速度大小为v0.
水平位移x=v0t,竖直位移y=
| 1 |
| 2 |
又tanθ=
| y |
| x |
联立得到,v0=
| gt |
| 2tanθ |
(2)设经过时间T,运动员的速度方向与斜面平行,此时运动员离斜面最远.则
vy=v0tanθ,又vy=gT
解得 T=1.5s
将运动员的平抛运动分解为平行于斜面方向与垂直于斜面方向,运动员在垂直于斜面方向做初速度大小为v0sinθ,加速度大小为-gcosθ的匀减速运动,则得到
运动员离斜坡的最大距离S=v0sinθT-
| 1 |
| 2 |
故答案为:20m/s;9m.
点评:本题第(1)问是常规题,抓住斜面的倾角反映位移的方向.第(2)问采用两种分解方法进行处理,难度较大.

练习册系列答案
相关题目
 (2010?北京)如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力.(取sin37°=0.60,cos37°=0.80;g取10m/s2)求:
(2010?北京)如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力.(取sin37°=0.60,cos37°=0.80;g取10m/s2)求: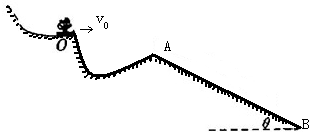 如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过t1=0.3s落到斜坡上的A点,速度平行于斜坡并刚好沿斜坡下滑.已知A点是斜坡的起点,B点是斜坡的终点,斜坡与水平面的夹角θ=37°,运动员与斜坡之间的滑动摩擦系数?=0.25,运动员通过斜坡AB的时间t2=6s,不计空气阻力.(取sin37°=0.60,cos37°=0.80;g取10m/s2)求
如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过t1=0.3s落到斜坡上的A点,速度平行于斜坡并刚好沿斜坡下滑.已知A点是斜坡的起点,B点是斜坡的终点,斜坡与水平面的夹角θ=37°,运动员与斜坡之间的滑动摩擦系数?=0.25,运动员通过斜坡AB的时间t2=6s,不计空气阻力.(取sin37°=0.60,cos37°=0.80;g取10m/s2)求