题目内容
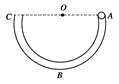
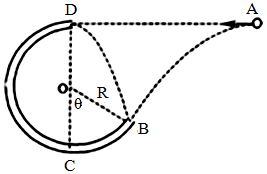
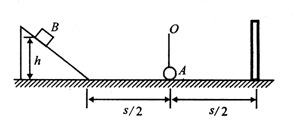
如图所示,质量为m=0.2kg的小物体放在光滑的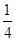 圆弧上端,圆弧半径R=55cm,下端接一长为1m的水平轨道AB,最后通过极小圆弧与倾角
圆弧上端,圆弧半径R=55cm,下端接一长为1m的水平轨道AB,最后通过极小圆弧与倾角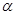 =37°的斜面相接,已知物体与水平面和斜面轨道的动摩擦因数均为0.1,将物体无初速度释放,求:
=37°的斜面相接,已知物体与水平面和斜面轨道的动摩擦因数均为0.1,将物体无初速度释放,求:

(1)物体第一次滑到圆弧底端A时对圆弧的压力为多少?
(2)物体第一次滑到水平轨道与右侧斜面轨道交接处B时的速度大小
(3)物体第一次滑上右侧斜轨道的最大高度(取g=10m/s2,cos37°=0.8,sin37°=0.6)
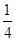 圆弧上端,圆弧半径R=55cm,下端接一长为1m的水平轨道AB,最后通过极小圆弧与倾角
圆弧上端,圆弧半径R=55cm,下端接一长为1m的水平轨道AB,最后通过极小圆弧与倾角 =37°的斜面相接,已知物体与水平面和斜面轨道的动摩擦因数均为0.1,将物体无初速度释放,求:
=37°的斜面相接,已知物体与水平面和斜面轨道的动摩擦因数均为0.1,将物体无初速度释放,求:
(1)物体第一次滑到圆弧底端A时对圆弧的压力为多少?
(2)物体第一次滑到水平轨道与右侧斜面轨道交接处B时的速度大小
(3)物体第一次滑上右侧斜轨道的最大高度(取g=10m/s2,cos37°=0.8,sin37°=0.6)
(1)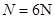 (2)
(2)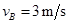 (3)
(3)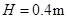
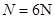 (2)
(2)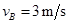 (3)
(3)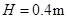
试题分析:(1)小物体第一次滑到圆弧底端时的速度大小为vA,由动能定理可得:
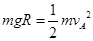 2分
2分解得
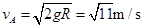 1分
1分在A点由牛顿第二定律可得;
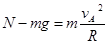 2分
2分解得
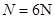 1分
1分由牛顿第三定律可得物体对圆弧轨道的压力大小为6N。 1分
(2)小物体从圆弧上端到B点的过程中,由动能定理有
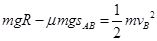 (1) 4分
(1) 4分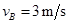 (3) 1分
(3) 1分(3)设物体第一次滑上右侧轨道最大高度为H此时物体离B点的距离为S,由几何关系有
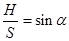 (4) 2分
(4) 2分由动能定理有
 (5) 2分
(5) 2分将(4)式代入(5)式,有
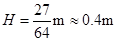 2分
2分
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目