题目内容
一块足够长的白板,位于水平桌面上,处于静止状态,一石墨块(可视为质点)静止在白板上,石墨块与白板间有摩擦,滑动摩擦系数μ=0.1。突然,使白板以恒定的加速度a1=2m/s2做匀加速直线运动,石墨块将在板上划下黑色痕迹,经过时间t=1s,令白板以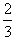 m/s2的加速度做匀减速直线运动直至静止。试求白板上黑色痕迹的长度(已知重力加速度为g=10m/s2,不计石墨与板摩擦划痕过程中损失的质量)。
m/s2的加速度做匀减速直线运动直至静止。试求白板上黑色痕迹的长度(已知重力加速度为g=10m/s2,不计石墨与板摩擦划痕过程中损失的质量)。
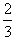 m/s2的加速度做匀减速直线运动直至静止。试求白板上黑色痕迹的长度(已知重力加速度为g=10m/s2,不计石墨与板摩擦划痕过程中损失的质量)。
m/s2的加速度做匀减速直线运动直至静止。试求白板上黑色痕迹的长度(已知重力加速度为g=10m/s2,不计石墨与板摩擦划痕过程中损失的质量)。解:设石墨块的加速度为a2 ,根据牛顿第二定律,得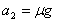 =1m/s2 ①
=1m/s2 ①
设经历时间t=1s,白板由静止开始加速到速度v1,石墨块则由静止加速到v2,有
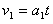 ②,
②,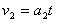 ③
③
由 ,故
,故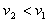 ,石墨块继续受到滑动摩擦力的作用
,石墨块继续受到滑动摩擦力的作用
设再经时间t',白板的速度由v1减小到v1',有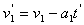 ④
④
石墨块的速度由v2增加到v2',有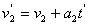 ⑤
⑤
当v1'=v2'后,即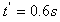 ,不再产生新的痕迹,然后两者共同减速运动至停止
,不再产生新的痕迹,然后两者共同减速运动至停止
设白板的速度从0增加到v1的过程中,白板和石墨块移动的距离分别为s1和s2
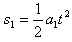 ⑥,
⑥,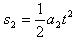 ⑦
⑦
在白板的速度从v1减小到v1'的过程中,白板和石墨块移动的距离分别为s1'和s2'
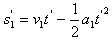 ⑧,
⑧, ⑨
⑨
传送带上留下的黑色痕迹的长度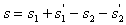 ⑩
⑩
由以上各式得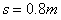
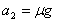 =1m/s2 ①
=1m/s2 ① 设经历时间t=1s,白板由静止开始加速到速度v1,石墨块则由静止加速到v2,有
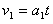 ②,
②,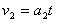 ③
③ 由
 ,故
,故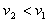 ,石墨块继续受到滑动摩擦力的作用
,石墨块继续受到滑动摩擦力的作用设再经时间t',白板的速度由v1减小到v1',有
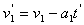 ④
④ 石墨块的速度由v2增加到v2',有
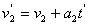 ⑤
⑤ 当v1'=v2'后,即
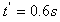 ,不再产生新的痕迹,然后两者共同减速运动至停止
,不再产生新的痕迹,然后两者共同减速运动至停止 设白板的速度从0增加到v1的过程中,白板和石墨块移动的距离分别为s1和s2
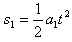 ⑥,
⑥,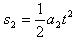 ⑦
⑦ 在白板的速度从v1减小到v1'的过程中,白板和石墨块移动的距离分别为s1'和s2'
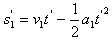 ⑧,
⑧, ⑨
⑨ 传送带上留下的黑色痕迹的长度
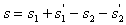 ⑩
⑩ 由以上各式得
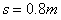

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目