题目内容
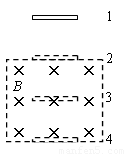
如图所示，空间某区域中有一匀强磁场，磁感应强度方向垂直纸面向里，磁场上、下边界分别位于水平面2、4处．在竖直面内有一矩形金属线圈，线圈上下边的距离很短，磁场上下边界之间的距离大于水平面1、2之间的距离．线圈下边位于水平面1处，由静止释放．若线圈下边刚通过水平面1、2、3（位于磁场中）和4时，线圈的加速度大小分别为a1、a2、a3和a4，且下落过程始终做加速运动，则（ ）
A．a1=a3＞a2＞a4
B．a1＜a2＜a3＜a4
C．a1＞a2＞a3＞a4
D．a1＞a3＞a4＞a2
【答案】分析：线圈未进入磁场时，只受重力，加速度为g．线圈进入磁场后，线圈受到重力和安培力作用，分析安培力公式推导出安培力与速度的关系，根据牛顿第二定律分析加速度大小．
解答：解：设线圈上下边长为l，磁感应强度为B，线圈电阻为R，当线圈速度为v，且有感应电流时，设线圈受到的安培力为F．
则有 F=
由题a1=g
线圈下边进入磁场时，根据牛顿定律，mg-F=ma2，F＜mg，则a2＜g
线圈位于磁场中运动时，没有感应电流，F=0，a3=g
由于线圈一直做加速运动，v4＞v2，则F4＞F2，a4＜a2．
综上得到a1=a3＞a2＞a4
故选A
点评：本题属于电磁感应中动态变化分析问题，关键是分析安培力与速度的关系，运用牛顿定律分析加速度的变化．
解答：解：设线圈上下边长为l，磁感应强度为B，线圈电阻为R，当线圈速度为v，且有感应电流时，设线圈受到的安培力为F．
则有 F=
由题a1=g
线圈下边进入磁场时，根据牛顿定律，mg-F=ma2，F＜mg，则a2＜g
线圈位于磁场中运动时，没有感应电流，F=0，a3=g
由于线圈一直做加速运动，v4＞v2，则F4＞F2，a4＜a2．
综上得到a1=a3＞a2＞a4
故选A
点评：本题属于电磁感应中动态变化分析问题，关键是分析安培力与速度的关系，运用牛顿定律分析加速度的变化．
练习册系列答案
相关题目
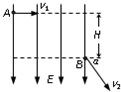如图所示，空间某区域存在竖直向下的匀强电场．带电小球质量为m，电量为q，在A点以水平向右的速度为v1射入电场，到B点时速度为v2，与水平方向的夹角为α．A、B间的高度差为H．以下判断错误的是（ ）
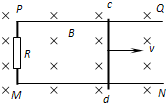如图所示，空间某区域存在水平方向的匀强磁场，磁感应强度B=1.0T．在磁场区域内有两根相距L=0.50m的平行金属导轨PQ、MN固定在竖直平面内，PM间连接有R=5.0Ω的电阻．当导体棒cd沿导轨平面向右匀速运动时，在闭合回路中产生的电流I=0.20A．求：
如图所示，空间某区域中有一匀强磁场，磁感应强度方向垂直纸面向里，磁场上、下边界分别位于水平面2、4处．在竖直面内有一矩形金属线圈，线圈上下边的距离很短，磁场上下边界之间的距离大于水平面1、2之间的距离．线圈下边位于水平面1处，由静止释放．若线圈下边刚通过水平面1、2、3（位于磁场中）和4时，线圈的加速度大小分别为a1、a2、a3和a4，且下落过程始终做加速运动，则（ ）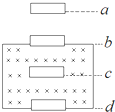
（2013?重庆二模）如图所示，空间某区域中有一匀强磁场，磁感应强度方向水平，且垂直于纸面向里，磁场上边界b和下边界d水平．在竖直面内有一矩形金属线框，线框上下边的距离很短，磁场上下边界之间的距离大于a、b之间的距离．线框从水平面a开始下落，当线框下边刚通过水平面b、c、d时，线框所受到的磁场力的大小分别为Fb、Fc和Fd，则（ ）