题目内容
（A）某天文台测得某行星的一颗卫星绕行星做匀速圆周运动，测得其轨道半径为R，周期为T，则其向心加速度为______；行星的质量为______．（万有引力恒量为G）
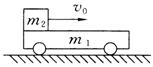
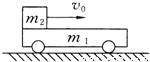
（B）如图所示，质量m1=0.3kg 的小车静止在光滑的水平面上，车长L=15m，现有质量m2=0.2kg可视为质点的物块，以水平向右的速度v0=2m/s从左端滑上小车，最后在车面上某处与小车保持相对静止．物块与车面间的动摩擦因数μ=0.5，则小车的最大速度是______ m/s；物块在车面上滑行的时间是______ s．
（B）如图所示，质量m1=0.3kg 的小车静止在光滑的水平面上，车长L=15m，现有质量m2=0.2kg可视为质点的物块，以水平向右的速度v0=2m/s从左端滑上小车，最后在车面上某处与小车保持相对静止．物块与车面间的动摩擦因数μ=0.5，则小车的最大速度是______ m/s；物块在车面上滑行的时间是______ s．
1、卫星的向心加速度a=Rω2=（
） 2 R．
根据G
=mR（
）2得，
M=
．
2、（1）依据动量守恒得 m2v0=（m1+m2）v
解得 v=0.8m/s
（2）物块所受的滑动摩擦力大小f=μm2g=1N
对小车，依据动量定理得 ft=m1v
解得t=0.24s
故答案为：1、(
)2R
2、0.8 0.24
| 2π |
| T |
根据G
| Mm |
| R2 |
| 2π |
| T |
M=
| 4π2R3 |
| GT2 |
2、（1）依据动量守恒得 m2v0=（m1+m2）v
解得 v=0.8m/s
（2）物块所受的滑动摩擦力大小f=μm2g=1N
对小车，依据动量定理得 ft=m1v
解得t=0.24s
故答案为：1、(
| 2π |
| T |
| 4π2R3 |
| GT2 |
2、0.8 0.24
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
（2011?静安区二模）（A）某天文台测得某行星的一颗卫星绕行星做匀速圆周运动，测得其轨道半径为R，周期为T，则其向心加速度为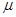
=0.5，则小车的最大速度是____ m/s；物块在车面上滑行的时间是_____ s。
