题目内容
(9分) 如图所示, 在距地面80 m高的水平面上做匀加速直线运动的飞机上每隔1 s依次放下M、N、P三物体, 抛出点a、b与b、c间距分别为45 m和55 m, 分别落在水平地面上的A、B、C处, g取10 m/s2。 求:
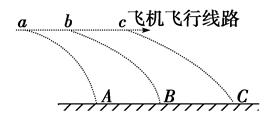
(1)飞机飞行的加速度;
(2)刚放下N物体时飞机的速度大小;
(3)N、P两物体落地点B、C间的距离。
(1)飞机飞行的加速度;
(2)刚放下N物体时飞机的速度大小;
(3)N、P两物体落地点B、C间的距离。
(1)10 m/s2 (2)50 m/s (3)95 m
(1)飞机在水平方向上, 由a经b到c做匀加速直线运动, 由Δs＝a0T2得,
a0＝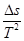
＝
＝10 m/s2.
(2)因位置b对应a到c过程的中间时刻, 故有
vb＝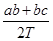
＝50 m/s.
(3)设物体落地时间为t,
由h＝
gt2
得: t＝
＝4 s
BC间的距离为: BC＝bc＋vct－vbt
又vc－vb＝a0T
得: BC＝bc＋a0Tt＝95 m.本题考查匀变速直线运动推论的应用，在匀变速直线运动过程中经过相邻的相等的时间内通过的位移差值恒定不变，由Δs＝a0T2可求得加速度大小，b点为a、c间的中间时刻，由中间时刻的瞬时速度等于平均速度可求得b点速度大小，自由落体运动中由公式Δs＝a0T2可求得BC段距离
a0＝
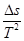＝＝10 m/s2.(2)因位置b对应a到c过程的中间时刻, 故有
vb＝
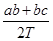＝50 m/s.(3)设物体落地时间为t,
由h＝
gt2得: t＝
＝4 sBC间的距离为: BC＝bc＋vct－vbt
又vc－vb＝a0T
得: BC＝bc＋a0Tt＝95 m.本题考查匀变速直线运动推论的应用，在匀变速直线运动过程中经过相邻的相等的时间内通过的位移差值恒定不变，由Δs＝a0T2可求得加速度大小，b点为a、c间的中间时刻，由中间时刻的瞬时速度等于平均速度可求得b点速度大小，自由落体运动中由公式Δs＝a0T2可求得BC段距离
练习册系列答案
智能训练练测考系列答案
相关题目
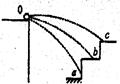
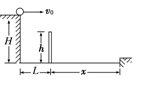
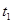，若给小球不同的水平初速度，落到斜面上的A点，经过的时间是
,落到斜面底端B点，经过的时间是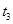
，落到水平面上的C点，经过的时间是
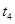，则（ ）
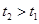
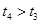
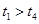
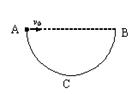
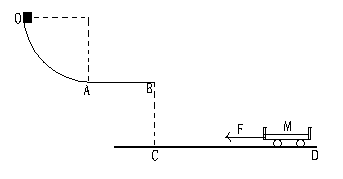
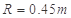，水平轨道AB长
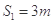，OA与AB均光滑。一滑块从O点由静止释放，当滑块经过A点时，静止在CD上的小车在
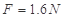的水平恒力作用下启动，运动一段时间后撤去力
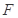。当小车在CD上运动了
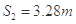时速度为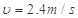
，此时滑块恰好落入小车中。已知小车质量
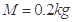，与CD间的动摩擦因数为
（
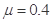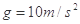）求：
