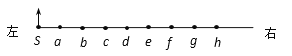题目内容
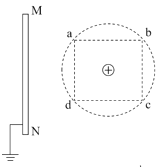
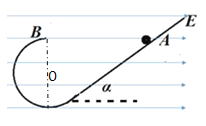
【题目】一个带正电荷量为q，质量为m的小球，恰能静止在光滑绝缘的斜面轨道上A点，已知半径为R的竖直圆形轨道与光滑斜面平滑对接，斜面倾角
，为使小球能到圆周轨道的最高点B，需要给小球提供一个初速度v。取重力加速度为g，开始A、B等高。求
（1）电场强度为多大？
（2）为使小球能通过B点，初速度v至少多大？
（3）在（2）的情况下取最小值v，则小球到B点时速度多大？
【答案】（1）
（2）
（3）
【解析】
在A点，小球受重力、水平向右的电场力和垂直轨道向上的弹力，根据平衡条件知
，
解得：
要使小球能通过B点，则小球能通过等效最高点，设等效最高点速度为v，根据牛顿第二定律有
，
解得：
，
从A到等效最高点根据动能定理有：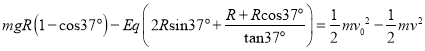
解得：；
取最小值v的情况下，由A到B由动能定理有：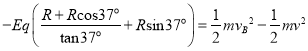
解得：
练习册系列答案
阅读快车系列答案
相关题目
【题目】某一研究性学习小组的同学们设计了以下实验方案来验证电荷守恒定律：
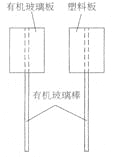
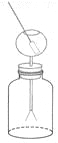
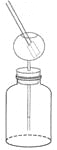
实 | 步骤一：手持起电板柄，用力将两块起电板快速摩擦后分开 | 步骤二：将其中一块板插入箔片验电器上端的空心金属球（不要接触金属球） | 步骤三：将两块板同时插入空心金属球 |
实 |
|
|
|
实 | 箔片张开 | 箔片闭合 |
根据以上实验过程和观察到的现象，回答下列问题：
（1）步骤二的实验现象，说明_____________________________________________
（2）步骤三的实验现象，说明_____________________________________________
（3）该研究性实验_________（填“能”或“不能”）验证电荷守恒定律。