题目内容
【题目】如图(1)所示,倾角为θ(θ<45°)的斜面ABC固定在水平地面上,置于斜面上的滑块P恰能沿斜面匀速下滑,已知滑块P从斜面顶端滑至底端的过程中,重力势能减小量为K.重力加速度为g.现将该斜面逆时针旋转90°后仍固定在水平地面上(如图(2)所示),在滑块P从斜面顶端由静止释放下滑至底端的过程中,能求出滑块 ( )
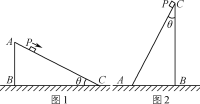
A.下滑至底端时的速度
B.下滑过程中的加速度
C.下滑至底端时的动能
D.下滑至底端时重力的功率
【答案】BC
【解析】
AC.设AB=h.滑块P恰能沿斜面匀速下滑时,有
mgsinθ=μmgcosθ
得
μ=tanθ
据重力势能减小量为K得
mgh=K
该斜面逆时针旋转90°后,根据动能定理
![]()
联立解得
![]()
![]()
由于m未知,所以根据mgh=K不能求出h,因此v求不出来,可求滑块下滑至底端时的动能Ek,故A错误,C正确;
B.根据牛顿第二定律得
mgcosθ-μmgsinθ=ma
得
a=gcosθ-gtanθsinθ
可以求出加速度a,故B正确;
D.滑块下滑至底端时重力的功率为
P=mgvcosθ
m和v都求不出来,则P求不出来,故D错误。
故选BC。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目