题目内容
【题目】如图所示,两端带有固定薄挡板的长木板C的长度为L,总质量为![]() ,与地面间的动摩擦因数为μ,其光滑上表面静置两质量分别为m、
,与地面间的动摩擦因数为μ,其光滑上表面静置两质量分别为m、![]() 的物体A、B,其中两端带有轻质弹簧的A位于C的中点。现使B以水平速度2v0向右运动,与挡板碰撞并瞬间粘连而不再分开,A、B可看作质点,弹簧的长度与C的长度相比可以忽略,所有碰撞时间极短,重力加速度为g,求:
的物体A、B,其中两端带有轻质弹簧的A位于C的中点。现使B以水平速度2v0向右运动,与挡板碰撞并瞬间粘连而不再分开,A、B可看作质点,弹簧的长度与C的长度相比可以忽略,所有碰撞时间极短,重力加速度为g,求:
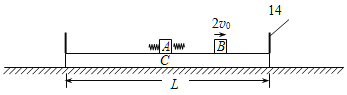
(1)B、C碰撞后瞬间的速度大小;
(2)A、C第一次碰撞时弹簧具有的最大弹性势能。
【答案】(i)![]() ;(ii)
;(ii)![]()
【解析】
试题分析:(1)B、C碰撞过程系统动量守恒,以向右为正方向,
由动量守恒定律得:![]()
解得:![]()
(2)对BC,由牛顿第二定律得:
设A、C第一次碰撞前瞬间C的速度为v2
有: ![]() ②
②
当A与B和C第一次碰撞具有共同速度v3时,弹簧的弹性势能最大,
系统动量守恒,以向右为正方向,由动量守恒定律得:
mv2=2mv3 ③
由能量守恒定律得:![]() ④
④
由①~④式解得:
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】用速度传感器研究匀变速直线运动的实验中,测得小车经过各时刻的瞬时速度如下:
时刻(s) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
瞬时速度(cm/s) | 44.0 | 62.0 | 81.0 | 100.0 | 118.0 | 138.0 |
为了求出加速度,最合理的方法是( )
A. 根据任意两个计数点的速度,用公式![]() 算出加速度
算出加速度
B. 根据实验数据画出v﹣t图象,量出其倾角θ,用公式a=tanθ算出加速度
C. 根据实验数据画出v﹣t图象,由较远两点所对应的速度及时间,用公式![]() 算出加速度
算出加速度
D. 依次算出通过连续两个计数点间的加速度,算出平均值即为小车的加速度