题目内容
如图所示,P、Q两个相同的小球在同一个固定的圆台形空桶内,在两个不同高度的水平面上,沿光滑桶壁做匀速圆周运动。下列判断正确的是( )


| A.P、Q做圆周运动的周期相同 | B.P、Q对桶壁的压力大小相同 |
| C.P所受的向心力较大 | D.P做圆周运动的线速度较大 |
B
考点:
专题:牛顿第二定律在圆周运动中的应用.
分析:涉及物理量较多时,比较多个量中两个量的关系,必须抓住不变量,而后才能比较变量.
解答:解:对P、Q两球进行受力分析,两球均只受重力和漏斗给的支持力FN.
对P球由牛顿第二定律:
FNPsinα=mg----------------------①
FNPcosα=m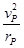 =mωP2rP-----------------------②
=mωP2rP-----------------------②
对Q球由牛顿第二定律:
FNQsinα=mg----------------------③
FNQcosα=m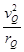 mωQ2rQ------------------------④
mωQ2rQ------------------------④
由两球质量相等可得FNP=FNQ,故B正确。 由②④可知,两球所受向心力相等.故C错误
m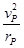 =m
=m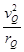 ,因为rP>rQ,所以vP>vQ, 故D错误。MωP2rP=mωQ2rQ,因为rP>rQ,所以ωP<ωQ,故又因为ω=
,因为rP>rQ,所以vP>vQ, 故D错误。MωP2rP=mωQ2rQ,因为rP>rQ,所以ωP<ωQ,故又因为ω=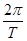 ,所以TP>TQ,故A错误
,所以TP>TQ,故A错误
故选B
点评:对物体进行受力分析,找出其中的相同的量,再利用圆周运动中各物理量的关系式分析比较,能较好的考查学生这部分的基础知识的掌握情况.
专题:牛顿第二定律在圆周运动中的应用.
分析:涉及物理量较多时,比较多个量中两个量的关系,必须抓住不变量,而后才能比较变量.
解答:解:对P、Q两球进行受力分析,两球均只受重力和漏斗给的支持力FN.
对P球由牛顿第二定律:
FNPsinα=mg----------------------①
FNPcosα=m
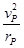 =mωP2rP-----------------------②
=mωP2rP-----------------------②对Q球由牛顿第二定律:
FNQsinα=mg----------------------③
FNQcosα=m
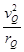 mωQ2rQ------------------------④
mωQ2rQ------------------------④由两球质量相等可得FNP=FNQ,故B正确。 由②④可知,两球所受向心力相等.故C错误
m
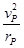 =m
=m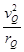 ,因为rP>rQ,所以vP>vQ, 故D错误。MωP2rP=mωQ2rQ,因为rP>rQ,所以ωP<ωQ,故又因为ω=
,因为rP>rQ,所以vP>vQ, 故D错误。MωP2rP=mωQ2rQ,因为rP>rQ,所以ωP<ωQ,故又因为ω=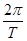 ,所以TP>TQ,故A错误
,所以TP>TQ,故A错误 故选B
点评:对物体进行受力分析,找出其中的相同的量,再利用圆周运动中各物理量的关系式分析比较,能较好的考查学生这部分的基础知识的掌握情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 向右做匀速运动,当小车遇到固定在地面的障碍物后,与之碰撞,碰后小车速度为零,关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )
向右做匀速运动,当小车遇到固定在地面的障碍物后,与之碰撞,碰后小车速度为零,关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )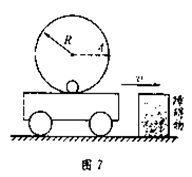



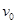 和位置s.
和位置s.


 和
和 同时系一质量为
同时系一质量为 的小球,且
的小球,且 ,两绳都拉直时与竖直方向的夹角分别为
,两绳都拉直时与竖直方向的夹角分别为 角和
角和 角,如图4所示。当小球以
角,如图4所示。当小球以 绕
绕 为轴转动时,上、下两绳的拉力分别是多少?
为轴转动时,上、下两绳的拉力分别是多少?