题目内容
2.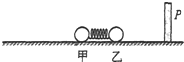 如图所示,足够长的光滑水平面上,两个静止的小球(甲和乙)将一轻质小弹簧压紧,弹簧弹性势能Ep=24J,小球甲的质量m1=3kg,小球乙的质量m2=1kg,小球乙右侧不远处有一挡板P.现将弹簧由静止释放,则:
如图所示,足够长的光滑水平面上,两个静止的小球(甲和乙)将一轻质小弹簧压紧,弹簧弹性势能Ep=24J,小球甲的质量m1=3kg,小球乙的质量m2=1kg,小球乙右侧不远处有一挡板P.现将弹簧由静止释放,则:(i)求弹簧恢复原长时甲和乙小球速度大小之比;
(ii)若小球乙与挡板P碰撞,反弹后甲乙两球刚好不再发生碰撞,求挡板P对小球乙的冲量大小.
分析 (1)根据动量守恒和机械能守恒列式,联立可求得最后速度,则可求得速度比值;
(2)根据题意可明确乙球的反弹后的速度,再由动量定理可求得冲量.
解答 解:(i)对两小球及弹簧组成的系统,动量守恒机械能守恒; 设向左为正方向,则有:m1v1=m2v2
EP=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22
联立两式解得:v1=2m/s,v2=6m/s;
故v1:v2=1:3;
(ii)反弹后甲乙两球刚好不发生碰撞,则说明反弹的乙球的速度大小为2m/s
则由动量定理可知:
挡板对小球的冲量大小为:
I=m2v3-m2(-v2)=1×2+1×6=8Ns
答:(i)弹簧恢复原长时甲和乙小球速度大小之比为1:3;
(ii)若小球乙与挡板P碰撞,反弹后甲乙两球刚好不再发生碰撞,挡板P对小球乙的冲量大小为8Ns.
点评 本题考查动量守恒定律以及动量定理的应用,要注意明确系统中能量的转化情况,同时注意明确动量、冲量及速度的矢量性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.两个相同的定值电阻 1、2 分别接在正弦交流电和直流电两端,直流电压恒为 U0.当电阻 1、2 的通电时间分别为 t 和 2t 时,两个电阻上产生的热量均为 Q.则该正弦交流电压的最大值是 ( )


| A. | $\frac{\sqrt{2}}{2}$U0 | B. | $\sqrt{2}$U0 | C. | U0 | D. | 2U0 |
13.A、B两只小球在空中某处,现同时以10m/s的速率抛出,A竖直上抛,B竖直下抛,不计空气阻力,g取10m/s2,则以下说法正确的是( )
| A. | 它们在运动过程中的平均速度相等 | |
| B. | 当它们落地时,在空中运动的位移大小相等 | |
| C. | 它们落地时间相差4s | |
| D. | 它们都在空中运动时,每秒钟它们之间的距离增加20m |
17. 如图所示,光滑竖直墙壁上有一颗钉子,分两次用长短不同的轻绳将同一个足球挂在该钉子上,足球分别静止在A、B两点;绳子拉力分别为TA和TB,墙对足球的支持力分别为NA和NB,则( )
如图所示,光滑竖直墙壁上有一颗钉子,分两次用长短不同的轻绳将同一个足球挂在该钉子上,足球分别静止在A、B两点;绳子拉力分别为TA和TB,墙对足球的支持力分别为NA和NB,则( )
 如图所示,光滑竖直墙壁上有一颗钉子,分两次用长短不同的轻绳将同一个足球挂在该钉子上,足球分别静止在A、B两点;绳子拉力分别为TA和TB,墙对足球的支持力分别为NA和NB,则( )
如图所示,光滑竖直墙壁上有一颗钉子,分两次用长短不同的轻绳将同一个足球挂在该钉子上,足球分别静止在A、B两点;绳子拉力分别为TA和TB,墙对足球的支持力分别为NA和NB,则( )| A. | TA<TB,NA<NB | B. | TA>TB,NA<NB | C. | TA<TB,NA>NB | D. | TA>TB,NA>NB |
7. 利用速度传感器与计算机结合,可以自动作出物体运动的图象.某同学在一次实验中得到的运动小车的速度-时间图象如图所示,以下说法中正确的是( )
利用速度传感器与计算机结合,可以自动作出物体运动的图象.某同学在一次实验中得到的运动小车的速度-时间图象如图所示,以下说法中正确的是( )
 利用速度传感器与计算机结合,可以自动作出物体运动的图象.某同学在一次实验中得到的运动小车的速度-时间图象如图所示,以下说法中正确的是( )
利用速度传感器与计算机结合,可以自动作出物体运动的图象.某同学在一次实验中得到的运动小车的速度-时间图象如图所示,以下说法中正确的是( )| A. | 小车做曲线运动 | B. | 小车运动的最大速度约为0.8 m/s | ||
| C. | 小车的位移一定大于8 m | D. | 小车先做加速运动,后做减速运动 |
14.大小为30N和40N的两个力的合力大小可能是( )
| A. | 5N | B. | 25N | C. | 70N | D. | 100N |
12.通过电阻R的电流为I时,在t时间内产生的热量为Q,若电阻为2R,通过的电流为2I,则在时间t内产生的热量为( )
| A. | 4Q | B. | 8Q | C. | $\frac{Q}{2}$ | D. | $\frac{Q}{4}$ |
 如图所示,在倾角为37°的光滑斜面上有一根长为0.4m,质量为6×10-2 kg的通电直导线,电流大小I=1A、方向垂直于纸面向外,导线用平行于斜面的轻绳拴住不动.
如图所示,在倾角为37°的光滑斜面上有一根长为0.4m,质量为6×10-2 kg的通电直导线,电流大小I=1A、方向垂直于纸面向外,导线用平行于斜面的轻绳拴住不动.