��Ŀ����
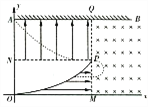
����Ŀ����ͼ��ʾ��OP���ߵķ���Ϊ��![]() ��x��y��λ��Ϊm������OPM�������ˮƽ���ҵ���ǿ�糡����ǿ��СE1=200 N/C����Ϊ��������MPQ�ұߴ��ڷ�Χ�㹻�����ǿ�ų����Ÿ�Ӧǿ��ΪB=0.1 T����Ϊ����������x��ƽ�е�PN�Ϸ�������PN��������ֱ���ϵ���ǿ�糡����ǿ��СE2=100 N/C����Ϊ��������PN���Ϸ�h=3.125 m����һ�㹻���Ľ���y��ˮƽ���õ�ӫ����AB��OM�ij���Ϊa=6.25 m����������OP��ͬʱ��ֹ�ͷ�����Ϊm=1.6��10��25 kg�������Ϊe=1.6��10��19 C�Ĵ��������2000������OP�ϰ�x���ȷֲ���������������֮�������ã���������������
��x��y��λ��Ϊm������OPM�������ˮƽ���ҵ���ǿ�糡����ǿ��СE1=200 N/C����Ϊ��������MPQ�ұߴ��ڷ�Χ�㹻�����ǿ�ų����Ÿ�Ӧǿ��ΪB=0.1 T����Ϊ����������x��ƽ�е�PN�Ϸ�������PN��������ֱ���ϵ���ǿ�糡����ǿ��СE2=100 N/C����Ϊ��������PN���Ϸ�h=3.125 m����һ�㹻���Ľ���y��ˮƽ���õ�ӫ����AB��OM�ij���Ϊa=6.25 m����������OP��ͬʱ��ֹ�ͷ�����Ϊm=1.6��10��25 kg�������Ϊe=1.6��10��19 C�Ĵ��������2000������OP�ϰ�x���ȷֲ���������������֮�������ã���������������![]() =2.5��������
=2.5��������
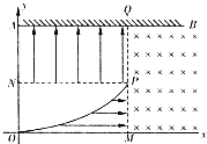
(1)��Щ���ӽ�������������ٶȴ�С��
(2)���Ӵ���ӫ�����ϵ����ߵij��Ⱥʹ���ӫ�����ϵ����Ӹ�����
(3)��Щ���Ӵӳ�������ӫ�����ϵ��ʱ�䣮
���𰸡���1����Щ���ӽ�������������ٶȴ�СΪ5��104 m/s��
��2�����Ӵ���ӫ�����ϵ����ߵij���6.25 m������ӫ�����ϵ�������500����
��3����Щ���Ӵӳ�������ӫ�����ϵ��ʱ��4.064��10-4 s��
��������
��1�������������˶����̸��ݶ��ܶ����з������ٶȵı���ʽ�������������ٶȣ�
��2���а뾶��ʽ��ʾ������������������Բ���˶��Ĺ���뾶�����ת����Ȧ�����ֱλ�ƣ�Ȼ������˶��ĺϳ���ֽ�������ڹ����ϵ����߳��ȣ����ݳ��ȱ����������
��3���ܴ�ӫ�����ϵ�������������ʱ������ֱ�������������˶�ʱ����������˶�ʱ����Բ���˶������ʱ�䣬��ͼ�Ϊ�ʱ�䣮
�⣺��1�������Ӵӵ㣨x��y��������eE1��a��x��=![]() mv02
mv02
![]()
��x=0ʱ�ٶ������������ٶ�vm=5��104m/s��
��2������������������Բ���˶��������뾶Ϊ��![]()
ת��Ȧ�����MQ���ϵ�C�㣬yc=2r+y=0.4![]() +y=1m
+y=1m
�������е����Ӿ�����P����ˮƽ���������ٶ���С�Ĵ�P�������ֱ�Ӵ���P�����Ϸ���ӫ�����ϣ��ٶ�������5��104m/s��ˮƽ�����������˶���
��ֱ�������ȼ���ֱ���˶���
a2=![]() =105m/s2
=105m/s2
t2=![]() =2.5��10��4s
=2.5��10��4s
������ƫ���y=vmt2=12.5m�������߳���Ϊ6.25m��������ȥ�ˣ�
����6.25m�������ӵ�ˮƽ�ٶ�Ϊ��v=![]() m/s=2.5��104m/s
m/s=2.5��104m/s
��v=![]() =2.5��104m/s
=2.5��104m/s
�ã�a��x=1.25
���Դ���ӫ�����ϵ�������n=![]() ��2000=500����
��2000=500����
��3���ܴ�ӫ�����ϵ��������������ʱ��Ϊt1
a1=![]() =2��105m/s2���ã�t2=
=2��105m/s2���ã�t2=![]() =1.25��10��4s
=1.25��10��4s
��������t��=![]() T=
T=![]() =3.14��10��5s
=3.14��10��5s
t=t1+t2+t��=4.064��10��4s