题目内容
水平地面上某物体，从A点无初速度以一定的加速度a1做匀加速直线运动．经过一段时间加速运动至B点后，立即以另一加速度a2做匀变速直线运动，经过与第一段时间两倍的时间，回到原出发点A点．则前、后两次加速度大小比值为（ ）
| A、1：3 | B、2：5 | C、3：5 | D、4：5 |
分析：根据匀变速直线运动的位移时间公式，结合时间关系，抓住两段过程中位移大小相等，求出两次加速度大小之比．
解答：解：匀加速直线运动的位移大小：x=
a1t2，匀加速直线运动的末速度为：v=a1t．
则匀变速直线运动的位移：x′=v?2t-
a2(2t)2．
根据x=-x′解得：
=
．故D正确，A、B、C错误．
故选：D．
| 1 |
| 2 |
则匀变速直线运动的位移：x′=v?2t-
| 1 |
| 2 |
根据x=-x′解得：
| a1 |
| a2 |
| 4 |
| 5 |
故选：D．
点评：解决本题的关键掌握匀变速直线运动的位移时间公式，注意公式的矢量性．
练习册系列答案
相关题目
（2011?无为县模拟）用水平力F拉着一物体在水平地面上做匀速运动，从某时刻起力F随时间均匀减小，物体所受的摩擦力f随时间t变化如图中实线所示．下列说法正确的是（ ）
如图所示，某物体以一定初动能Ek0沿固定在水平地面上的粗糙斜面从底端P点开始上滑，一段时间之后物体离开斜面做斜上抛运动，到达最高点Q，设斜面各部分粗糙程度均匀，取地面为零势能面，则关于物体从P到Q的运动过程中机械能随时间的变化关系E-t；及物体的动能随离地面的竖直高度的变化关系EK-h，下列图象描述正确的是（ ）
随时间t变化如下图中实线所示。下列说法正确的是（ ）
时刻开始减小的，
时刻物体的速度刚好变为零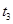
时刻物体的速度刚好变为零