题目内容
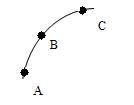
 如图所示,某物体以一定初动能Ek0沿固定在水平地面上的粗糙斜面从底端P点开始上滑,一段时间之后物体离开斜面做斜上抛运动,到达最高点Q,设斜面各部分粗糙程度均匀,取地面为零势能面,则关于物体从P到Q的运动过程中机械能随时间的变化关系E-t;及物体的动能随离地面的竖直高度的变化关系EK-h,下列图象描述正确的是( )
如图所示,某物体以一定初动能Ek0沿固定在水平地面上的粗糙斜面从底端P点开始上滑,一段时间之后物体离开斜面做斜上抛运动,到达最高点Q,设斜面各部分粗糙程度均匀,取地面为零势能面,则关于物体从P到Q的运动过程中机械能随时间的变化关系E-t;及物体的动能随离地面的竖直高度的变化关系EK-h,下列图象描述正确的是( )分析:物体在斜面上做匀减速直线运动,从斜面抛出后做斜抛运动,机械能的变化量等于除重力以外的力做的功,合外力做的功等于动能的变化量,写出机械能的表达式即可选择图象.
解答:解:A、在斜面上运动某一位置的机械能E=EK0-f×(v0t-
at2),从斜面抛出后,只有重力做功,机械能守恒,不发生变化,故A正确,B错误;
B、在斜面上运动某一位置的动能为:EK=EK0-(
+mg)h,在斜抛到最高点的过程中,某一位置的动能为:EK=EK1-mgh,
动能随高度的变化关系,从图象角度看是在斜面运动过程中的斜率大于斜抛过程中的斜率,且Q点动能不为零,故C错误,D正确.
故选AD
| 1 |
| 2 |
B、在斜面上运动某一位置的动能为:EK=EK0-(
| f |
| sinθ |
动能随高度的变化关系,从图象角度看是在斜面运动过程中的斜率大于斜抛过程中的斜率,且Q点动能不为零,故C错误,D正确.
故选AD
点评:本题主要考查了功能关系的直接应用,知道机械能的变化量等于除重力以外的力做的功,合外力做的功等于动能的变化量,注意在最高点竖直方向的速度等于零,水平方向速度不为零,难度适中.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目