题目内容
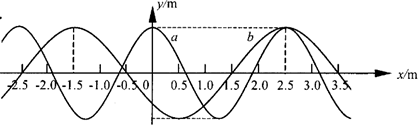
(08年上海卷)(12分)有两列简谐横波a、b在同一媒质中沿x轴正方向传播,波速均为v=2.5m/s。在t=0时,两列波的波峰正好在x=2.5m处重合,如图所示。
(1)求两列波的周期Ta和Tb。
(2)求t=0时,两列波的波峰重合处的所有位置。
(3)辨析题:分析并判断在t=0时是否存在两列波的波谷重合处。
某同学分析如下:既然两列波的波峰存在重合处,那么波谷与波谷重合处也一定存在。只要找到这两列波半波长的最小公倍数……即可得到波谷与波谷重合处的所有位置。
 你认为该同学的分析正确吗?若正确,求出这些点的位置。若不正确,指出错误处并通过计算说明理由。
你认为该同学的分析正确吗?若正确,求出这些点的位置。若不正确,指出错误处并通过计算说明理由。
解析:
(1)从图中可以看出两列波的波长分别为λa=2.5m,λb=4.0m,因此它们的周期分别为
![]() s=1s
s=1s ![]() s=1.6s
s=1.6s
(2)两列波的最小公倍数为 S=20m
t=0时,两列波的波峰相遇处的所有位置为
x=(2.5![]() 20k)m,k=0,1,2,3,……
20k)m,k=0,1,2,3,……
(3)该同学的分析不正确。
要找两列波的波谷与波谷重合处,必须从波峰重合处出发,找到这两列波半波长的厅数倍恰好相等的位置。设距离x=2.5m为L处两列波的波谷与波谷相遇,并设
L=(2m-1)![]() L=(2n-1),式中m、n均为正整数
L=(2n-1),式中m、n均为正整数
只要找到相应的m、n即可
将λa=2.5m,λb=4.0m代入并整理,得
![]()
由于上式中m、n在整数范围内无解,所以不存在波谷与波谷重合处。

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 A.绕O点顺时针方向转动
A.绕O点顺时针方向转动