题目内容
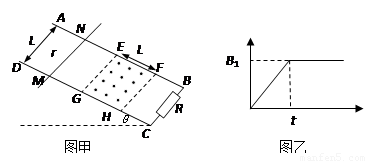
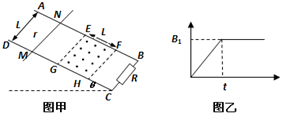
如图甲所示,平行光滑导轨AB、CD倾斜放置,与水平面间的夹角为θ,间距为L,导轨下端B、C间用电阻R=2r相连.一根质量为m、电阻为r的导体棒MN垂直放在导轨上,与导轨接触良好,方向始终平行于水平地面.在导轨间的矩形区域EFGH内存在长度也为L、垂直于导轨平面向上的匀强磁场,磁感应强度随时间变化的规律如图乙所示.t=0时刻由静止释放导体棒MN,恰好在t1时刻进入磁场EFGH并做匀速直线运动.求:
(1)导体棒MN进入磁场前,电阻R两端的电压U;
(2)导体棒MN在磁场中匀速运动时的速度v和电阻匀速运动过程中R上产生的焦耳热Q.
(1)导体棒MN进入磁场前,电阻R两端的电压U;
(2)导体棒MN在磁场中匀速运动时的速度v和电阻匀速运动过程中R上产生的焦耳热Q.

分析:(1)导体棒MN进入磁场前,穿过EFHG的磁场磁感应强度均匀增大,回路中产生恒定的感应电动势和感应电流,根据法拉第电磁感应定律和欧姆定律求出回路中的感应电流,由部分电路欧姆定律求电阻R两端的电压U;
(2)导体棒MN进入磁场后,以速度v作匀速直线运动,受力平衡,根据平衡条件和安培力公式列式,求解v.由焦耳定律求出R上产生的焦耳热Q.
(2)导体棒MN进入磁场后,以速度v作匀速直线运动,受力平衡,根据平衡条件和安培力公式列式,求解v.由焦耳定律求出R上产生的焦耳热Q.
解答:解:(1)导体棒MN进入磁场前,回路MNBC中产生感生电动势:ε1=
=L2
根据闭合电路欧姆定律得:I=
电阻R两端的电压为:U=I?2r=
(2)导体棒MN进入磁场后,以速度v作匀速直线运动,磁场为B1稳恒不变,感应电动势为:
ε2=B1Lv
导体棒中的电流强度为:I=
由导体棒MN受力平衡,得:mgsinθ=B1IL
解得:v=
导体棒在磁场中运动的时间为:t=
则电阻R上产生的焦耳热为:Q=I2?2rt=
mgLsinθ
答:
(1)导体棒MN进入磁场前,电阻R两端的电压U是
;
(2)导体棒MN在磁场中匀速运动时的速度v是
,电阻匀速运动过程中R上产生的焦耳热Q是
mgLsinθ.
| △φ |
| △t |
| B1 |
| t1 |
根据闭合电路欧姆定律得:I=
| ε1 |
| 3r |
电阻R两端的电压为:U=I?2r=
| 2B1L2 |
| 3t1 |
(2)导体棒MN进入磁场后,以速度v作匀速直线运动,磁场为B1稳恒不变,感应电动势为:
ε2=B1Lv
导体棒中的电流强度为:I=
| ε2 |
| 3r |
由导体棒MN受力平衡,得:mgsinθ=B1IL
解得:v=
| 3mgrsinθ |
| B12L2 |
导体棒在磁场中运动的时间为:t=
| L |
| v |
则电阻R上产生的焦耳热为:Q=I2?2rt=
| 2 |
| 3 |
答:
(1)导体棒MN进入磁场前,电阻R两端的电压U是
| 2B1L2 |
| 3t1 |
(2)导体棒MN在磁场中匀速运动时的速度v是
| 3mgrsinθ | ||
|
| 2 |
| 3 |
点评:本题中先产生感生电动势,要会运用法拉第定律求感应电动势.导体棒进入磁场后,产生动生电动势,由E=BLv求解感应电动势.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
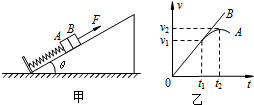 如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接;两物块A、B质量均为m,初始时物块均静止.现用平行于斜面向上的拉力F拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图乙所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则( )
如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接;两物块A、B质量均为m,初始时物块均静止.现用平行于斜面向上的拉力F拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图乙所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则( )A、A达到最大速度时的位移
| ||||
| B、拉力F的最小值为mgsinθ+ma | ||||
C、A、B分离时t1=
| ||||
| D、A、B分离前,A、B和弹簧系统机械能增加,A和弹簧系统机械能增加 |
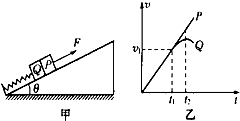 如图甲所示,平行于斜面的轻弹簧,劲度系数为k,一端固定在在倾角为θ 的斜面底端,另一端与Q物块连接,P、Q质量均为m,斜面光滑且固定在水平面上,初始时物块均静止.现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,两个物块在开始一段时间内的v-t图象如图乙所示(重力加速度为g),则下列说法不正确的是( )
如图甲所示,平行于斜面的轻弹簧,劲度系数为k,一端固定在在倾角为θ 的斜面底端,另一端与Q物块连接,P、Q质量均为m,斜面光滑且固定在水平面上,初始时物块均静止.现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,两个物块在开始一段时间内的v-t图象如图乙所示(重力加速度为g),则下列说法不正确的是( )| A、平行于斜面向上的拉力F一直增大 | ||
| B、外力施加的瞬间,P、Q间的弹力大小为m(gsinθ-a) | ||
C、从O开始到t1时刻,弹簧释放的弹性势能为
| ||
| D、t2时刻弹簧恢复到原长,物块Q达到速度最大值 |
 如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接;两物块A、B质量均为m,初始时物块均静止.现用平行于斜面向上的拉力F拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图乙所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则( )
如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接;两物块A、B质量均为m,初始时物块均静止.现用平行于斜面向上的拉力F拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图乙所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则( )| A、外力施加的瞬间,A、B间的弹力大小为m(gsinθ-a) | ||
B、t2时刻,弹簧形变量为
| ||
| C、t2时刻弹簧恢复到原长,物块A达到速度最大值 | ||
D、从开始到t1时刻,拉力F做的功比弹簧释放的势能少
|
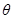 ,间距为L,导轨下端B、C间用电阻R=2r相连。一根质量为m、电阻为r的导体棒MN垂直放在导轨上,与导轨接触良好,方向始终平行于水平地面。在导轨间的矩形区域EFGH内存在长度也为L、垂直于导轨平面向上的匀强磁场,磁感应强度随时间变化的规律如图乙所示。t=0时刻由静止释放导体棒MN,恰好在t1时刻进入磁场EFGH并做匀速直线运动。求:
,间距为L,导轨下端B、C间用电阻R=2r相连。一根质量为m、电阻为r的导体棒MN垂直放在导轨上,与导轨接触良好,方向始终平行于水平地面。在导轨间的矩形区域EFGH内存在长度也为L、垂直于导轨平面向上的匀强磁场,磁感应强度随时间变化的规律如图乙所示。t=0时刻由静止释放导体棒MN,恰好在t1时刻进入磁场EFGH并做匀速直线运动。求: