Question

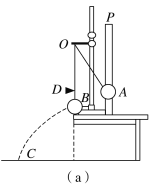
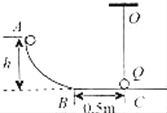
【题目】光滑曲面AB与滑动摩擦系数μ=0.4的粗糙水平面BC相切于B点，如图所示．图中SBC =0.5m，用细线拴一质量M =1kg小球Q，细线长L =1.5m，细线的另一端悬于O点，球Q在C点时，对C点无压力.质量m =1kg的小球P自高h =1.0m处沿曲面AB由静止开始滑下，在水平面上与球Q正碰，若碰撞过程中无机械能损失（g取10m/s2），求P与Q第一次碰撞后，P的速度和小球Q上升的最大高度H.

Answer 1

【答案】0，0.8m

【解析】 (1)P球从开始下滑到碰撞前的过程，运用动能定理得

P球和Q球在碰撞过程中，取向右为正方向，由动量守恒定律和能量守恒定律得

由机械能守恒定律得：

解得：vP=0,vQ=4m/s

设P与Q第一次碰撞后小球Q上升的最大高度为H.

对Q，由机械能守恒定律得

联立解得H=0.8m