题目内容
14.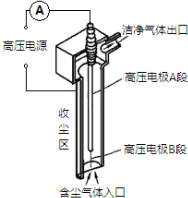 空气中直径小于等于2.5 微米的细颗粒物称做PM2.5,其在空气中的含量称作PM值,单位是毫克每立方米.某校“PM2.5兴趣小组”自制了一台静电除尘器,装置呈圆筒形,如图为其截面图.高压电极的负极位于中轴线上,由A、B两段金属构成,A段较粗呈杆状,B段较细呈针状,收尘区由半径为R的圆柱形的金属筒壁构成,接高压电源的正极.圆筒中气体分子中的电子和带正电的部分由于受到方向相反的强大的静电力而电离.一部分细颗粒物吸附了电子而带负电,所有带负电的细颗粒物都飞向筒壁,最后在重力的作用下落在筒底,空气因此而变得清洁.在一次试验中,含尘气体由底部吹入,气流速度恒为v,高压电源的恒定不变,工作电流恒为I,经监测,入口处的含尘气体的PM值为k1,出口处的洁净气体的PM值降为k2,若视细颗粒物均为直径为D、密度为ρ的均匀球体,且不计相互之间的影响,忽略含尘气体带入的电荷.
空气中直径小于等于2.5 微米的细颗粒物称做PM2.5,其在空气中的含量称作PM值,单位是毫克每立方米.某校“PM2.5兴趣小组”自制了一台静电除尘器,装置呈圆筒形,如图为其截面图.高压电极的负极位于中轴线上,由A、B两段金属构成,A段较粗呈杆状,B段较细呈针状,收尘区由半径为R的圆柱形的金属筒壁构成,接高压电源的正极.圆筒中气体分子中的电子和带正电的部分由于受到方向相反的强大的静电力而电离.一部分细颗粒物吸附了电子而带负电,所有带负电的细颗粒物都飞向筒壁,最后在重力的作用下落在筒底,空气因此而变得清洁.在一次试验中,含尘气体由底部吹入,气流速度恒为v,高压电源的恒定不变,工作电流恒为I,经监测,入口处的含尘气体的PM值为k1,出口处的洁净气体的PM值降为k2,若视细颗粒物均为直径为D、密度为ρ的均匀球体,且不计相互之间的影响,忽略含尘气体带入的电荷.(1)电离主要发生在高压电极的A段附近还是B段附近,并且简述理由;
(2)求细颗粒物平均吸附的电子个数n和抵达收尘区时的平均动能E.
分析 (1)电场强度越大的地方气体越容易电离.
(2)由电荷守恒定律与PM值可以求出电子个数,由动能定理求出颗粒的动能.
解答 解:(1)中轴线上的金属与与圆柱形桶壁间的电压相同,A段较粗呈杆状,B段较细呈针状,B段附近的电场较强,电场越强,空气越容易电离,因此电离主要发生在B段附近,因为B段附近电场比A段附近的电场更强.
(2)设收尘区长度为l,颗粒的运动时间:t=$\frac{l}{v}$,电荷量:Q=It=I×$\frac{l}{v}$,
颗粒个数:N=$\frac{2π{R}^{2}l({k}_{1}-{k}_{2})}{ρ•\frac{4}{3}π(\frac{D}{2})^{3}}$=$\frac{12{R}^{2}l({k}_{1}-{k}_{2})}{ρ{D}^{3}}$,
颗粒吸附的电子电荷量:Q=Nne=$\frac{12n{eR}^{2}l({k}_{1}-{k}_{2})}{ρ{D}^{3}}$,
则:I×$\frac{l}{v}$=$\frac{12n{eR}^{2}l({k}_{1}-{k}_{2})}{ρ{D}^{3}}$,解得:n=$\frac{ρI{D}^{3}}{12ev{R}^{2}({k}_{1}-{k}_{2})}$;
由动能定理得:neU=E-0,解得:E=$\frac{ρI{D}^{2}U}{12v{R}^{2}({k}_{1}-{k}_{2})}$;
答:(1)电离主要发生在B段附近,因为B段附近电场比A段附近的电场更强.
(2)细颗粒物平均吸附的电子个数n为:$\frac{ρI{D}^{3}}{12ev{R}^{2}({k}_{1}-{k}_{2})}$,抵达收尘区时的平均动能E为:$\frac{ρI{D}^{2}U}{12v{R}^{2}({k}_{1}-{k}_{2})}$.
点评 本题考查了空气的电离、求颗粒浮电子的个数、颗粒的动能,知道电场越强空气越容易电离,应用电流的定义式、密度公式、动能定理即可正确解题,本题是一道创新题,难度较大.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案 2013年6月10日上午,我国首次太空授课在距地球300多千米的“天空一号”上举行,如图所示的是宇航员王亚萍在“天空一号”上所做的“水球”.下列关于“水球”和“天空一号”的说法正确的是( )
2013年6月10日上午,我国首次太空授课在距地球300多千米的“天空一号”上举行,如图所示的是宇航员王亚萍在“天空一号”上所做的“水球”.下列关于“水球”和“天空一号”的说法正确的是( )| A. | “水球”的形成是因为太空中没有重力 | |
| B. | “水球”的向心加速度小于5m/s2 | |
| C. | “天空一号”运行速度小于7.9km/s | |
| D. | “天宫一号”的角速度比同步卫星的大 |
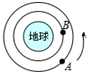
| A. | B卫星比A卫星运行周期小 | |
| B. | A卫星在图示位置加速后有可能会撞上B卫星 | |
| C. | A卫星的运行速度一定小于地球的第一宇宙速度 | |
| D. | 可以通过A卫星的运行周期和万有引力常量计算出地球的质量 |
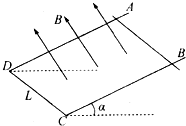 如图所示,一个U形导体框架,其宽度L=1m,框架平面与水平面夹角α=30°,其电阻可忽略不计,设匀强磁场的磁感应强度与U形框架的平面垂直.匀强磁场的磁感应强度B=0.2T.今有一条形导体AB,其质量为m=0.5kg,有效电阻R=0.1Ω,跨接在U形框架上,并能无摩擦地滑动.求:
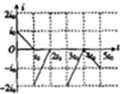
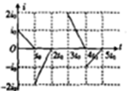
如图所示,一个U形导体框架,其宽度L=1m,框架平面与水平面夹角α=30°,其电阻可忽略不计,设匀强磁场的磁感应强度与U形框架的平面垂直.匀强磁场的磁感应强度B=0.2T.今有一条形导体AB,其质量为m=0.5kg,有效电阻R=0.1Ω,跨接在U形框架上,并能无摩擦地滑动.求: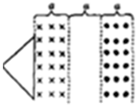 如图所示,两个匀强磁场区域的宽度均为a,中间无磁场区域的宽度也为a,匀强磁场区域的磁感应强度大小相等,方向相反,现有斜边长为$\sqrt{2}$a的等腰直角三角形导线框,从图示位置开始以水平向右的恒定速度穿越该场区,若以线框中逆时针方向为电流正方向,则图中能正确描述该过程线框中感应电流i与时间t的关系的是( )
如图所示,两个匀强磁场区域的宽度均为a,中间无磁场区域的宽度也为a,匀强磁场区域的磁感应强度大小相等,方向相反,现有斜边长为$\sqrt{2}$a的等腰直角三角形导线框,从图示位置开始以水平向右的恒定速度穿越该场区,若以线框中逆时针方向为电流正方向,则图中能正确描述该过程线框中感应电流i与时间t的关系的是( )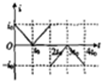

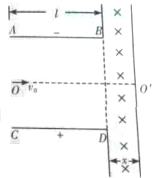 如图所示,长为l=1m的平行板电容器,AB和CD两板的间距也为l.两板的带电性质如图.某粒子源沿平行板中心轴线发射出速度都为v0=2×104m/s的比荷为1×104C/kg的正粒子.在平行板的右侧有3个荧光屏,分别放置在AB板B的边缘上方,CD板D边缘下方和距离BD右边x=$\frac{0.2}{\sqrt{3}}$m处,且足够大,屏和平行板垂直,如图所示,在BD和右板之间的区域内有磁感应强度大小B=0.1T的匀强磁场,磁场方向垂直纸面向里.不考虑粒子的重力,认为平行板内为匀强电场,板外无电场.(答案可用根号表示).
如图所示,长为l=1m的平行板电容器,AB和CD两板的间距也为l.两板的带电性质如图.某粒子源沿平行板中心轴线发射出速度都为v0=2×104m/s的比荷为1×104C/kg的正粒子.在平行板的右侧有3个荧光屏,分别放置在AB板B的边缘上方,CD板D边缘下方和距离BD右边x=$\frac{0.2}{\sqrt{3}}$m处,且足够大,屏和平行板垂直,如图所示,在BD和右板之间的区域内有磁感应强度大小B=0.1T的匀强磁场,磁场方向垂直纸面向里.不考虑粒子的重力,认为平行板内为匀强电场,板外无电场.(答案可用根号表示).