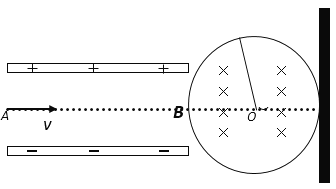
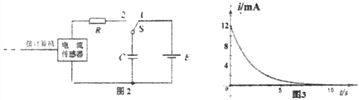
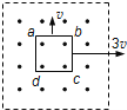
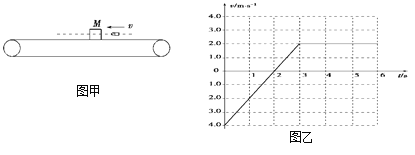
题目内容
【题目】如图所示为一滑梯的实物图,滑梯的斜面段长度L=5.0m,倾角θ=37°,水平段与斜面段平滑连接。某小朋友从滑梯顶端由静止开始滑下,经斜面底端后水平滑行一段距离,停在滑梯轨道上。已知小朋友质量为m=20kg,小朋友与滑梯轨道间的动摩擦因数μ=0.3,sin37°=0.60,cos37°=0.80,g取10m/s2,不计空气阻力。求:

(1)小朋友沿滑梯斜面段下滑时所受摩擦力的大小;
(2)小朋友滑到斜面底端时的速度大小;
(3)若用一拉力将小朋友拉回滑梯顶端,拉力方向与轨道始终平行,拉力做功的最小值是多少。
【答案】(1)f=48N (2)v=6m/s (3)W=1200J
【解析】(1)小孩在斜面上滑行时所受的摩擦力大小为:Ff=μmgcosθ=0.3×20×10×cos37°=48N;
(2)小孩在斜面上滑行时,由牛顿第二定律得:mgsinθ-μmgcosθ=ma1
解得:a1=3.6m/s2,
由匀变速直线运动的速度位移公式:v2-v02=2ax可知,
小孩滑至B点时的速度大小为:![]()
(3)小孩在水平段滑行时,由动能定理得:![]()
可得![]()
下滑过程:![]()
重力做功:![]()
拉回小朋友回顶端至少需要克服重力做功、两端的摩擦力做功
则![]()

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目