题目内容
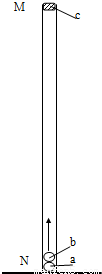
两端开口、内壁光滑的直玻璃管MN竖直固定在水平面上,a、b二个小球,直径相等,略小于玻璃管的内径,且远小于玻璃管的长度,大小可忽略不计;a、b两球的质量分别为m1和m2(m1=2m2).开始时,a球在下b球在上两球紧挨着在管口M处由静止同时释放,a球着地后立即反弹,其速度大小不变,方向竖直向上,与b球相碰,接着b球竖直上升.设两球碰撞时间极短、碰撞过程中总动能不变,在b球开始上升的瞬间,一质量为m3的橡皮泥在M处自由落下,如图所示.b与c在管中某处相遇后粘在一起,要使b、c粘合后能够竖直飞出玻璃管口,则m2与m3之比必须满足什么条件?
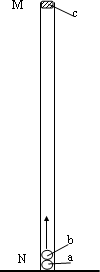
答案:
解析:
解析:
|
解:设管长为H,取向下为正方向,则a、b两球到达玻璃管底端时,速度都为 a球着地后反弹,速度为 a、b两球相碰,总动量守恒 总动能守恒 联立①至④式,并代入m1=2m2,解得 设c在M处下落经t时间后与b相碰,则 碰撞前b、c的速度分别为 b与c相碰,总动量守恒 要使b、c粘合体能飞出管口,则c与b碰后的速度必须竖直向上,且大小大于 得 解得b、c两者质量之比为 因此要使b、c粘合后能够竖直飞出玻璃管口,必须满足条件 评分标准:①至④式各1分,⑤式4分;⑥至⑧式每式2分,⑨、⑩式每式1分,最后结论2分. |

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
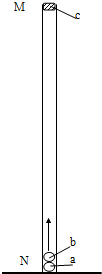 (2008?广州模拟)两端开口、内壁光滑的直玻璃管MN竖直固定在水平面上,a、b二个小球,直径相等,略小于玻璃管的内径,且远小于玻璃管的长度,大小可忽略不计;a、b两球的质量分别为m1和m2(m1=2m2).开始时,a球在下b球在上两球紧挨着在管口M处由静止同时释放,a球着地后立即反弹,其速度大小不变,方向竖直向上,与b球相碰,接着b球竖直上升.设两球碰撞时间极短、碰撞过程中总动能不变,在b球开始上升的瞬间,一质量为m3的橡皮泥在M处自由落下,如图所示.b与c在管中某处相遇后粘在一起,要使b、c粘合后能够竖直飞出玻璃管口,则m2与m3之比必须满足什么条件?
(2008?广州模拟)两端开口、内壁光滑的直玻璃管MN竖直固定在水平面上,a、b二个小球,直径相等,略小于玻璃管的内径,且远小于玻璃管的长度,大小可忽略不计;a、b两球的质量分别为m1和m2(m1=2m2).开始时,a球在下b球在上两球紧挨着在管口M处由静止同时释放,a球着地后立即反弹,其速度大小不变,方向竖直向上,与b球相碰,接着b球竖直上升.设两球碰撞时间极短、碰撞过程中总动能不变,在b球开始上升的瞬间,一质量为m3的橡皮泥在M处自由落下,如图所示.b与c在管中某处相遇后粘在一起,要使b、c粘合后能够竖直飞出玻璃管口,则m2与m3之比必须满足什么条件?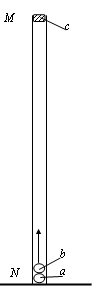
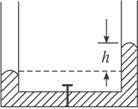
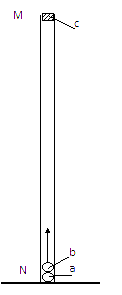 两端开口、内壁光滑的直玻璃管MN竖直固定在水平面上,a、b二个小球,直径相等,略小于玻璃管的内径,且远小于玻璃管的长度,大小可忽略不计;a、b两球的质量分别为m1和m2(m1 = 2m2)。开始时,a球在下b球在上两球紧挨着在管口M处由静止同时释放,a球着地后立即反弹,其速度大小不变,方向竖直向上,与b球相碰,接着b球竖直上升。设两球碰撞时间极短、碰撞过程中总动能不变,在b球开始上升的瞬间,一质量为m3的橡皮泥在M处自由落下,如图所示。b与c在管中某处相遇后粘在一起,要使b、c粘合后能够竖直飞出玻璃管口,则m2与m3之比必须满足什么条件?
两端开口、内壁光滑的直玻璃管MN竖直固定在水平面上,a、b二个小球,直径相等,略小于玻璃管的内径,且远小于玻璃管的长度,大小可忽略不计;a、b两球的质量分别为m1和m2(m1 = 2m2)。开始时,a球在下b球在上两球紧挨着在管口M处由静止同时释放,a球着地后立即反弹,其速度大小不变,方向竖直向上,与b球相碰,接着b球竖直上升。设两球碰撞时间极短、碰撞过程中总动能不变,在b球开始上升的瞬间,一质量为m3的橡皮泥在M处自由落下,如图所示。b与c在管中某处相遇后粘在一起,要使b、c粘合后能够竖直飞出玻璃管口,则m2与m3之比必须满足什么条件?