Question

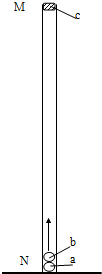（2008?广州模拟）两端开口、内壁光滑的直玻璃管MN竖直固定在水平面上，a、b二个小球，直径相等，略小于玻璃管的内径，且远小于玻璃管的长度，大小可忽略不计；a、b两球的质量分别为m₁和m₂（m₁=2m₂）．开始时，a球在下b球在上两球紧挨着在管口M处由静止同时释放，a球着地后立即反弹，其速度大小不变，方向竖直向上，与b球相碰，接着b球竖直上升．设两球碰撞时间极短、碰撞过程中总动能不变，在b球开始上升的瞬间，一质量为m₃的橡皮泥在M处自由落下，如图所示．b与c在管中某处相遇后粘在一起，要使b、c粘合后能够竖直飞出玻璃管口，则m₂与m₃之比必须满足什么条件？

Answer 1

分析：两球落到底端后相碰的过程中动量守恒，机械能守恒，根据动量守恒、机械能守恒求出碰后两球的速度，根据位移公式求出b、c相碰前的速度，结合动量守恒定律求出碰后的速度，要使b、c粘合体能飞出管口，则c与b碰后的速度必须竖直向上，且大小大于C碰撞前的速度，根据该关系求出m₂与m₃之比必须满足的条件．

解答：解：设管长为H，取向下为正方向，则a、b两球到达玻璃管底端时，速度都为v0=

2gH

①
a球着地后反弹，速度为va1=-v0=-

2gH

②
a、b两球相碰，总动量守恒   m₁v_a1+m₂v₀=m₁v_a2+m₂v_b1
总动能守恒  

1

2

m1

v

2 a1

+

1

2

m2

v

2 0

=

1

2

m1

v

2 a2

+

1

2

m2

v

2 b1

④
联立①至④式，并代入m₁=2m₂，解得   va2=

1

3

v0，vb1=-

5

3

v0⑤
设c在M处下落经t时间后与b相碰，则-(vb1t+

1

2

gt2)+

1

2

gt2=H解得   t=

H

-vb1

⑥
碰撞前b、c的速度分别为 vb2=vb1+gt=

41

9

?

gH

vb1

⑦
b与c相碰，总动量守恒   m₂v_b2+m₃v_c1=（m₂+m₃）v_bc⑧
要使b、c粘合体能飞出管口，则c与b碰后的速度必须竖直向上，且大小大于v_c1，取v_bc=-v_c1，代入上式，
得  m2?

41

9

?

gH

vb1

-m3?

gH

vb1

=(m2+m3)

gH

vb1

⑨
解得b、c两者质量之比为    

m2

m3

=

9

16

⑩
因此要使b、c粘合后能够竖直飞出玻璃管口，必须满足条件 

m2

m3

＞

9

16

．
答：必须满足条件

m2

m3

＞

9

16

．

点评：本题综合考查了动量守恒守恒定律、能量守恒定律以及运动学公式，综合性较强，对学生的能力要求较高，是一道难题，关键理清运动过程，选择合适的规律进行求解．